Common Nonlinear Regression Models - Intrinsically Linear Regression Models

Polynomial Regression
A common "nonlinear" model is polynomial regression. We put the term nonlinear in quotes here because the nature of this model is actually linear. For example, suppose we measure in a learning experiment subjects' physiological arousal and their performance on a complex tracking task. Based on the well-known Yerkes-Dodson law we could expect a curvilinear relationship between arousal and performance; this expectation can be expressed in the regression equation:

Performance = a + b1*Arousal + b2*Arousal2

In this equation, a represents the intercept, and b1 and b2 are regression coefficients. The non-linearity of this model is expressed in the term Arousal2. However, the nature of the model is still linear, except that when estimating it, we would square the measure of arousal. The Multiple Regression fixed nonlinear option could also be used to estimate the regression coefficients for this model. These types of models, where we include some transformation of the independent variables in a linear equation, are also referred to as models that are nonlinear in the variables.

Models that are nonlinear in the parameters
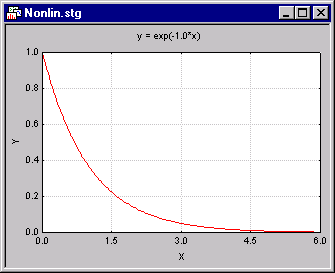
To contrast the example above, consider the relationship between a human's age from birth (the x variable) and his or her growth rate (the y variable). Clearly, the relationship between these two variables in the first year of a person's life (when most growth occurs) is very different than during adulthood (when almost no growth occurs). Thus, the relationship could probably best be expressed in terms of some negative exponential function:

Growth = exp(-b1*Age)

If you plotted this relationship for a particular estimate of the regression coefficient you would obtain a curve that looks something like this.

Note: the nature of this model is no longer linear, that is, the expression shown above does not simply represent a linear regression model, with some transformation of the independent variable. This type of model is said to be nonlinear in the parameters.
Making nonlinear models linear
In general, whenever a regression model can be "made" into a linear model, this is the preferred route to pursue (for estimating the respective model). The linear multiple regression model (see Multiple Regression) is very well understood mathematically, and, from a pragmatic standpoint, is most easily interpreted. Therefore, returning to the simple exponential regression model of Growth as a function of Age shown above, we could convert this nonlinear regression equation into a linear one by simply taking the logarithm of both sides of the equations, so that:

log(Growth) = -b1*Age

If we now substitute log(Growth) with y, we have the standard linear regression model as shown earlier (without the intercept which was ignored here to simplify matters). Thus, we could log-transform the Growth rate data (e.g., using the spreadsheet formula transformations) and then use Multiple Regression to estimate the relationship between Age and Growth, that is, compute the regression coefficient b1.

Model adequacy. Of course, by using the "wrong" transformation, one could end up with an inadequate model. Therefore, after "linearizing" a model such as the one shown above, it is particularly important to use the extensive residual statistics in Multiple Regression.