Basic Ideas - Interaction Effects
There is another advantage of ANOVA over simple t-tests: ANOVA allows us to detect interaction effects between variables, and, therefore, to test more complex hypotheses about reality. Let us consider another example to illustrate this point. (The term interaction was first used by Fisher, 1926.)
Main effects, two-way interaction
Imagine that we have a sample of highly achievement-oriented students and another of achievement "avoiders." We now create two random halves in each sample, and give one half of each sample a challenging test, the other an easy test. We measure how hard the students work on the test. The means of this (fictitious) study are as follows:
How can we summarize these results? Is it appropriate to conclude that (1) challenging tests make students work harder, (2) achievement-oriented students work harder than achievement-avoiders? None of these statements captures the essence of this clearly systematic pattern of means. The appropriate way to summarize the result would be to say that challenging tests make only achievement-oriented students work harder, while easy tests make only achievement-avoiders work harder. In other words, the type of achievement orientation and test difficulty interact in their effect on effort; specifically, this is an example of a two-way interaction between achievement orientation and test difficulty. Note that statements 1 and 2 above describe so-called main effects.
Higher order interactions
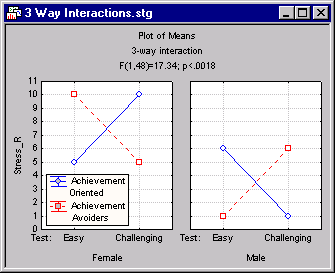
While the previous two-way interaction can be put into words relatively easily, higher order interactions are increasingly difficult to verbalize. Imagine that we had included factor Gender in the achievement study above, and we had obtained the following pattern of means:
| Females | Achievement-oriented | Achievement-avoiders |
| Challenging Test | 10 | 5 |
| Easy Test | 5 | 10 |
| Males | Achievement-oriented | Achievement-avoiders |
| Challenging Test | 1 | 6 |
| Easy Test | 6 | 1 |
How could we now summarize the results of our study? ANOVA/MANOVA allows you to produce graphs of means for all effects with basically a single click of the mouse; those graphs greatly facilitate the interpretation of complex effects. The pattern shown in the table above (and in the graph below) represents a three-way interaction between factors.
Thus we can summarize this pattern by saying that for females there is a two-way interaction between achievement-orientation type and test difficulty: Achievement-oriented females work harder on challenging tests than on easy tests, achievement-avoiding females work harder on easy tests than on difficult tests. For males, this interaction is reversed. As you can see, the description of the interaction has become much more involved.
A general way to express interactions
A general way to express all interactions is to say that an effect is modified (qualified) by another effect. Let us try this with the two-way interaction above. The main effect for test difficulty is modified by achievement orientation. For the three-way interaction in the previous paragraph, we may summarize that the two-way interaction between test difficulty and achievement orientation is modified (qualified) by Gender. If we have a four-way interaction, we may say that the three-way interaction is modified by the fourth variable, that is, that there are different types of interactions in the different levels of the fourth variable. As it turns out, in many areas of research five- or higher-way interactions are not that uncommon.