GC&RT Introductory Overview - Basic Ideas Part II
Advantages of Classification and Regression Trees (C&RT) Methods
As mentioned earlier, there are a large number of methods that an analyst can choose from (and they are all available in the STATISTICA system) when analyzing classification or regression problems. Tree classification techniques, when they "work" and produce accurate predictions or predicted classifications based on few logical if-then conditions, have a number of advantages over many of those alternative techniques.
- Simplicity of results
- In most cases, the interpretation of results summarized in a tree is very simple. This simplicity is useful not only for purposes of rapid classification of new observations (it is much easier to evaluate just one or two logical conditions, than to compute classification scores for each possible group, or predicted values, based on all predictors and using possibly some complex nonlinear model equations), but can also often yield a much simpler "model" for explaining why observations are classified or predicted in a particular manner (e.g., when analyzing business problems, it is much easier to present a few simple if-then statements to management, than some elaborate equations; compare, for example, the result shown in this section for the regression tree analysis of the Poverty data set with the results presented in the context of Example 1 of the Multiple Regression Analysis module).
- Tree methods are nonparametric and nonlinear
- The final results of using tree methods for classification or regression can be summarized in a series of (usually few) logical if-then conditions (tree nodes). Therefore, there is no implicit assumption that the underlying relationships between the predictor variables and the dependent variable are linear, follow some specific non-linear link function [e.g., see Generalized Linear/Nonlinear Models (GLZ)], or that they are even monotonic in nature. For example, some continuous outcome variable of interest could be positively related to a variable Income if the income is less than some certain amount, but negatively related if it is more than that amount (i.e., the tree could reveal multiple splits based on the same variable Income, revealing such a non-monotonic relationship between the variables). Thus, tree methods are particularly well suited for data mining tasks, where there is often little a priori knowledge nor any coherent set of theories or predictions regarding which variables are related and how. In those types of data analyses, tree methods can often reveal simple relationships between just a few variables that could have easily gone unnoticed using other analytic techniques.
General Computation Issues and Unique Solutions of STATISTICA GC&RT
The computational details involved in determining the best split conditions to construct a simple yet useful and informative tree are quite complex. Refer to Breiman et al. (1984) for a discussion of their CART ® algorithm to learn more about the general theory of and specific computational solutions for constructing classification and regression trees; STATISTICA's GC&RT module implements those techniques and extends them in several ways (see also the discussion of ANCOVA-like predictor designs). An excellent general discussion of tree classification and regression methods, and comparisons with other approaches to pattern recognition and neural networks, is provided in Ripley (1996). Computational Details also provides in some detail how the C&RT algorithm works. What follows is a brief discussion of some computational solutions and unique features of STATISTICA C&RT.
Avoiding Over-Fitting: Pruning, cross-validation, and V-fold cross-validation
A major issue that arises when applying regression or classification trees to "real" data with much random error noise concerns the decision when to stop splitting. For example, if you had a data set with 10 cases, and performed 9 splits (determined 9 if-then conditions), you could perfectly predict every single case. In general, if you only split a sufficient number of times, eventually you will be able to "predict" ("reproduce" would be the more appropriate term here) your original data (from which you determined the splits). Of course, it is far from clear whether such complex results (with many splits) will replicate in a sample of new observations; most likely they will not.
This general issue is also discussed in the literature on tree classification and regression methods, as well as neural networks, under the topic of "overlearning" or "overfitting." If not stopped, the tree algorithm will ultimately "extract" all information from the data, including information that is not and cannot be predicted in the population with the current set of predictors, i.e., random or noise variation. The general approach to addressing this issue is first to stop generating new split nodes when subsequent splits only result in very little overall improvement of the prediction. For example, if you can predict 90% of all cases correctly from 10 splits, and 90.1% of all cases from 11 splits, then it obviously makes little sense to add that 11th split to the tree. STATISTICA offers many such criteria for automatically stopping the splitting (tree-building) process, and they are further described in Computational Details.
Once the tree building algorithm has stopped, it is always useful to further evaluate the quality of the prediction of the current tree in samples of observations that did not participate in the original computations. These methods are used to "prune back" the tree, i.e., to eventually (and ideally) select a simpler tree than the one obtained when the tree building algorithm stopped, but one that is equally as accurate for predicting or classifying "new" observations.
- cross-validation
- One approach (further detailed in Computational Details) is to apply the tree computed from one set of observations (learning sample) to another completely independent set of observations (testing sample). If most or all of the splits determined by the analysis of the learning sample are essentially based on "random noise," then the prediction for the testing sample will be very poor. Hence one can infer that the selected tree is not very good (useful), and not of the "right size."
- V-fold cross-validation
- Continuing further along this line of reasoning (described in the context of cross-validation above), why not repeat the analysis many times over with different randomly drawn samples from the data, for every tree size starting at the root of the tree, and applying it to the prediction of observations from randomly selected testing samples. Then use (interpret, or accept as your final result) the tree that shows the best average accuracy for cross-validated predicted classifications or predicted values. In most cases, this tree will not be the one with the most terminal nodes, i.e., the most complex tree. This method for pruning a tree, and for selecting a smaller tree from a sequence of trees, can be very powerful, and is particularly useful for smaller data sets (see also Computational Details or the description of the Quick Specs dialog - Validation tab for further details). It is an essential step for generating useful (for prediction) tree models, and because it can be computationally difficult to do, this method is often not found in tree classification or regression software. However, STATISTICA's GC&RT (as well as GCHAID) can accommodate these techniques.
Reviewing Large Trees: Unique Analysis Management Tools
Another general issue that arises when applying tree classification or regression methods is that the final trees can become very large. In practice, when the input data are complex and, for example, contain many different categories for classification problems and many possible predictors for performing the classification, then the resulting trees can become very large. This is not so much a computational problem as it is a problem of presenting the trees in a manner that is easily accessible to the data analyst, or for presentation to the "consumers" of the research.
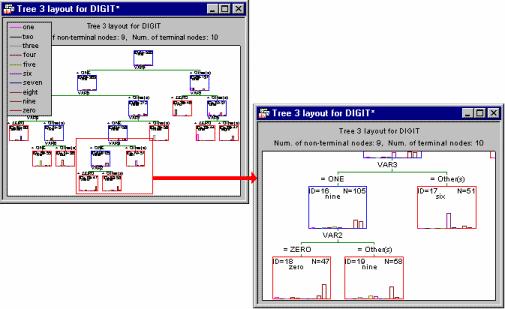
STATISTICA offers three ways in which complex trees can be reviewed. Like all graphs in STATISTICA, the tree chart summarizing the final solution (tree) can be "navigated" using the standard zooming tools. So for example, you can quickly zoom into an area of a larger tree that is of particular interest, and use the zoom pan button to move around the graph (see also Navigating (zooming on) the summary tree graph, below).
- Point-and-click tools for tree graphs
- You can also click the Brush tree button on the Summary tab of the Results dialog and use the cross-hair tool
to select individual nodes of the tree. As you move the crosshair over a node in the tree, a ToolTip will pop up to display summary statistics for that node.
Click on a node to select (highlight) it, and then choose any of the options from the floating ("brushing") toolbar or the shortcut menu for that node.
- Scrollable tree window
- You can also display the summary tree graph in a scrollable window.
In a sense, this method allows you to move a (resizable) window over a much larger tree graph.
- Tree Browser
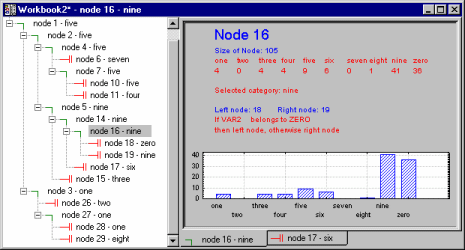
- However, the most convenient way (and most standard way, from the user-interface point of view) to review information in trees is via the tree browser. In STATISTICA GC&RT (as well as
GCHAID), the final tree can be reviewed in an efficient workbook tree browser.
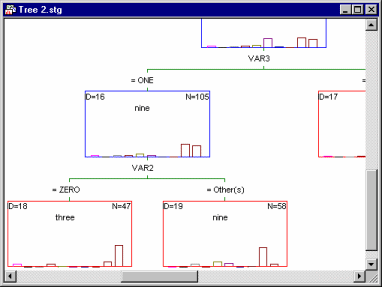
For example, the illustration above was taken from an analysis of the Digit.sta example data set (see also Classification Trees Analysis Example 1: Discriminant-Based Univariate Splits for Categorical Predictors; or Example 1: Pattern Recognition). The goal of the analysis was to accurately predict a single digit number (between 0 and 9) from 7 "noisy" predictors (for a description of how these data were generated, see Breiman et. al., 1984). The final tree results are displayed in the workbook tree browser, which clearly identifies the splitting nodes (
) and terminal nodes (
) of the tree. To review the statistics and other information (e.g., splitting rule) associated with each node, simply highlight it and review the summary graph in the right pane. In the example above, split Node 16 identifies a split on Var2: If it is equal to 0, then the respective observations are classified to Node 18 (i.e., they are identified as digit Zero); if Var2 is not equal to 0, then the respective observations are classified as Nine.
The split nodes can be collapsed or expanded, in the manner that most users are accustomed to from standard MS Windows-style tree-browser controls. This is the most efficient method for reviewing complex tree models, and at this time STATISTICA is the only program that incorporates this necessary device to review and present results.
Another useful feature of the workbook tree browser is the ability to quickly review the effect of consecutive splits on the resulting child nodes in an "animation-like" manner. For example, shown below is the summary result from a regression-like analysis. Place the mouse pointer in the left pane and select (highlight) the root node, and then use the arrow keys on your keyboard to move down as the splits are added to the tree.
The splitting of the overall sample into sub-groups (nodes) of increasing purity (homogeneity, or smaller variance) is evident in this illustration.
Navigating (zooming on) the summary tree graph. Of course, you can also navigate the traditional summary tree graph, using the standard STATISTICA zooming tools.
These tools can be used to review all details of large and complex tree graphs.
The classic (Breiman et. al., 1984) classification and regression trees algorithms can accommodate both continuous and categorical predictor variables (see also, Computational Details). However, in practice, it is not uncommon to combine such variables into analysis of variance/covariance (ANCOVA) like predictor designs with main effects or interaction effects for categorical and continuous predictors. This method of analyzing coded ANCOVA-like designs is relatively new and, to date, only available in STATISTICA GC&RT as well as GCHAID. However, it is easy to see how the use of coded predictor designs expands these powerful classification and regression techniques to the analysis of data from experimental designs (e.g., see for example the detailed discussion of experimental design methods for quality improvement in the context of the Experimental Design module of Industrial Statistics).
Note: the user interface and methods for specifying designs in GC&RT are identical to those used in GLM, GRM, GLZ, PLS, and GDA (a comprehensive description of the analysis syntax for specifying ANOVA/ANCOVA-like designs is presented in the context of GLM). Hence, a great advantage of this method for analyzing data is that identical predictor designs can be applied using these very different methods for analyzing regression-type problems [e.g., via General Linear Models (GLM), various Generalized Linear/Nonlinear Models (GLZ), Partial Least Squares (PLS) methods, or General CHAID Models (GCHAID)] or classification-type problems [e.g., via General CHAID Models (GCHAID),General Discriminant Analysis (GDA) models, or applicable Generalized Linear/Nonlinear Models (GLZ)].Note: there are four different types of tree-building algorithms available in STATISTICA: CHAID (Kass (1980; see General CHAID Introductory Overview), C&RT (Breiman, Friedman, Olshen, and Stone, 1984; see General Classification and Regression Trees), and QUEST (Loh and Shih, 1997; see Classification Trees Analysis); see also CHAID, C & RT, and QUEST for additional details.
