Data Relationships Anova Algorithm 

The Anova option computes the difference between groups by comparing the mean values of the data in each group. The results are obtained by testing the null hypothesis; the hypothesis that there is no difference between the means of the groups. More formally, the p-value is the probability of the actual or a more extreme outcome under the null-hypothesis.

Note: If there are empty values in the data table, the data table will first be reduced to the rows containing values for both the first and the second column.

For each combination of category and value column, a p-value is computed as follows:

1. Rows are grouped according to their value in the category column.

2. The total mean value of the value column is computed.
    

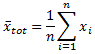
3. The mean within each group is computed.

4. The difference between each value and the mean value for the group is calculated and squared.

5. The squared difference values are added. The result is a value that relates to the total deviation of rows from the mean of their respective groups. This value is referred to as the sum of squares within groups, or S2Wthn.

6. For each group, the difference between the total mean and the group mean is squared and multiplied by the number of values in the group. The results are added. The result is referred to as the sum of squares between groups, or S2Btwn.
   

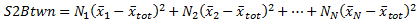
7. The two sums of squares are used to obtain a statistic for testing the null hypothesis, the so called F-statistic. The F-statistic is calculated as:
   
   
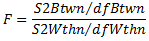
   where dfBtwn (degree of freedom between groups) equals the number of groups minus 1, and dfWthn (degree of freedom within groups) equals the total number of values minus the number of groups.

8. The F-statistic is distributed according to the F-distribution (commonly presented in mathematical tables/handbooks). The F-statistic, in combination with the degrees of freedom and an F-distribution table, yields the p-value.

The p-value is the probability of the actual or a more extreme outcome under the null-hypothesis. The lower the p-value, the larger the difference.

Note: A very small p-value may also arise if an effect is tiny but the sample sizes are large. Similarly, a higher p-value can arise if the effect is large but the sample size is small. This is because the hypothesis tests whether the effect is zero or not.