Elastic-Net Linear Regression
The Elastic-Net Linear Regression operator applies the elastic-net linear regression algorithm to the input data set. This operator supports the open source implementation of the elastic-net regularized linear regression algorithm.

Information at a Glance
|
Parameter |
Description |
|---|---|
| Category | Model |
| Data source type | TIBCO® Data Virtualization |
| Send output to other operators | Yes |
| Data processing tool | TIBCO® DV, Apache Spark 3.2 or later |
Algorithm
The Elastic-Net Linear Regression operator fits a trend line to an observed data set where one of the data values (dependent variable) is linearly dependent on the value of the other causal data values or variables (independent variables). This operator implements the elastic-net linear regression in Spark MLlib.
A Penalizing parameter (lambda) and the Elastic parameter (alpha) are applied to prevent the chances of overfitting the model. You can use this operator to optimize the best combination of alpha and lambda with a cross-validation method. This operator is limited by the cluster resources and Spark data frame size. One-hot encoding of high-cardinality categorical columns is limited by Spark cluster size.
Input
An input is a single tabular data set.
Bad or Missing Values
Configuration
The following table provides the configuration details for the Elastic-Net Linear Regression operator.
| Parameter | Description |
|---|---|
| Notes | Notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk appears on the operator. |
| Dependent Variable | Specify the categorical data columns as the dependent column. It must be numerical and the value cannot be a label or class. |
| Use all available columns as Predictors | When set to Yes, the operator uses all the available columns as predictors and ignores the Continuous Predictors and Categorical Predictors parameters. When set to No, the user must select at least one of the Continuous or Categorical Predictors. |
| Continuous Predictors |
Specify the numerical data columns as independent columns. It must be numerical column. Click Select Columns to select the required columns. Note:
The columns selected in the Categorical Predictors parameter are not available. |
| Categorical Predictors |
Specify the categorical data columns as independent columns. Note:
The columns selected in the Continuous Predictors parameter are not available. |
| Normalize Numerical Features |
Specify whether to normalize numerical features using Z-Transformation. Default: Yes |
| Evaluation Metric | Specify the metric for evaluating the regression models such as MAE, MSE, R2, and RMSE. Default: RMSE |
| Iterations |
Specify the maximum number of iterations for each grid of parameters. Default: 100 |
| Tolerance |
Specify the convergence tolerance. Default: 0.01 |
| Penalizing Parameter (λ) |
The λ parameter grid for Lasso Regression. For more information, see Classification and Regression in the Apache Spark documentation. The following values are valid:
Values of λ should span different orders of magnitude. In the case of start: end: count(n), Team Studio creates an exponential grid of n λ values from start to end.
Default: 0.0, 0.5, 2 |
| Elastic Parameter (α) |
The parameter to control the ElasticNet parameter.
For more information, see Linear Methods - RDD-based API. The following are valid values:
If start > end, then "Not valid; start value of alpha is greater than the end value" is returned. If step > (end - start), then "Not valid; check the step value" is returned. Default: 0.0, 0.5, 0.1 |
| Number of Cross Validation Folds |
Specify the number of cross-validation samples. Default: 3 |
| Random Seed |
Specify the seed used for the pseudo-random row extraction. Default: 1 |
Output
-
Parameter Summary Info: Displays a list of the input parameters and their current settings.
-
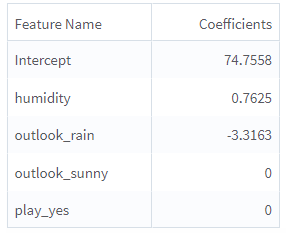
Coefficients: Displays the coefficient of the model.
-
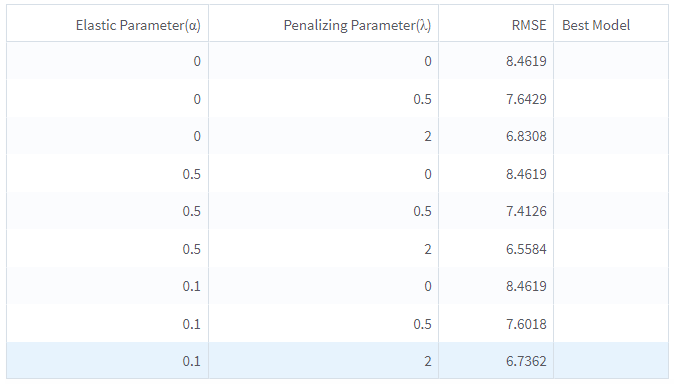
Training Summary: Displays a table with a row for each tested combination of hyper-parameters. For each hyper-parameter, the chosen metric is displayed and the Best Model is marked.
-
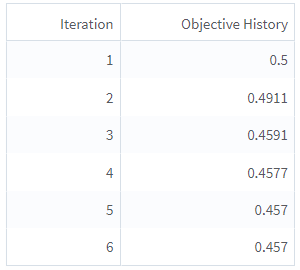
Objective History: Displays a table showing the evolution of the objective function value during optimization. The objective function is the elastic-net objective function of linear regression with selected alpha and lambda:
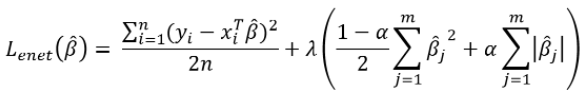
For Spark ML elastic-net linear regression, the default optimization method is L-BFGS, a numerical optimization algorithm. The training process stops once the difference between two consecutive iterations is smaller than the user-specified tolerance.
In the case the exact solution of the objective function is obtained, the optimization method is the normal equation method. For example, when the value of lambda is 0, regularization is not applied to the objective function. In this case, the elastic-net linear regression is equivalent to the ordinary linear regression. An exact solution is obtained by the normal equation method. In another case, when alpha is 0, the exact solution is derivable. In this scenario, the elastic-net loss is equivalent to the ridge loss. The ridge loss is a convex function where a unique solution exists. In this case, the normal equation method is applied.
For more information, see Optimization of linear methods.
Example
The following example demonstrates the Elastic-Net Linear Regression operator.
golf: This data set contains the following information:
- Multiple columns namely outlook, temperature, wind, humidity, and play.
- Multiple rows (14 rows).
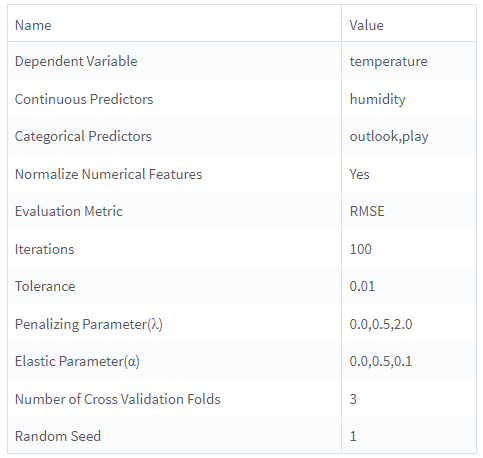
The parameter settings for the golf data set are as follows:
-
Dependent Variable: temperature
-
Use all available columns as Predictors: No
-
Continuous Predictors: humidity
-
Categorical Predictors: outlook, play
-
Normalize Numerical Features: Yes
-
Evaluation Metric: RMSE
-
Iterations: 100
-
Tolerance: 0.01
-
Penalizing Parameter (λ): 0.0, 0.5, 2
-
Elastic Parameter (α): 0.0, 0.5, 0.1
- Number of Cross Validation Folds: 3
- Random Seed: 1
The following figures display the results for the parameter settings for the golf data set.