PCA
The Principal Component Analysis (PCA) operator generates an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables.

Information at a Glance
|
Parameter |
Description |
|---|---|
| Category | Model |
| Data source type | TIBCO® Data Virtualization |
| Send output to other operators | Yes |
| Data processing tool | TIBCO® DV, Apache Spark 3.2 or later |
Algorithm
The PCA is an orthogonal linear transformation that transforms data into a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, the third on the third coordinate, continuing until the number of coordinates has been reached or a preset maximum principal component threshold has been reached.
This operator applies Center and Scale transformation to the selected columns, before generating the principal components. It also generates the full number of principal components.
Input
An input is a single tabular data set.
Bad or Missing Values
When null values are encountered in a column of a specific row, the entire row is removed before training a PCA model.
Configuration
The following table provides the configuration details for the PCA operator.
| Parameter | Description |
|---|---|
| Notes | Notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk appears on the operator. |
| Continuous Predictors |
Specify the numerical data columns as independent columns. It must be numerical column. Click Select Columns to select the required columns. |
| Use all available columns as Predictors | When set to Yes, the operator enable the wildcard feature. When set to No, users must select at least one of the Continuous Predictors. |
Output
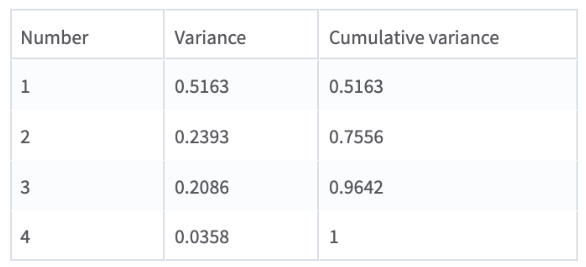
- Components: Displays the component matrix used for generating the principal components.
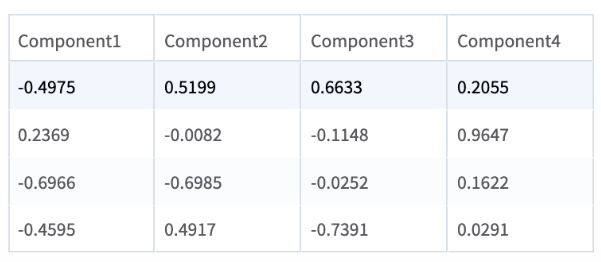
- Variance: Captures information on variance explained by each principal component (in descending order) alongside a cumulative total of variance explained.
A model object that can be used with a Predictor operator. The PCA operator outputs the principal components and not the transformed data set. To perform the transformation against a data set, the PCA operator must be succeeded by a Predictor operator. This operator adds p transformed columns, where p is the number of selected columns. The transformations are then processed against the source training data set or a new input data set with the same variables.
When the PCA operator is used with the Predictor operator in Team Studio, the number of components in the output is the same as the number of input columns. The users must review the Variance tab in the visual output to identify the amount of variance to capture and consequently the number of principal components to store. Based on this information, users can attach a Dynamic Column Filter operator to the output of the Predictor operator to keep only the required variables.
Example
The following example demonstrates the PCA operator.

demographics: This data set contains the following information:
- Sepal length
- Sepal width
- Petal length
- Petal width
Parameter Setting
The parameter settings for the demographics data set are as follows:
-
Continuous Predictors: sepal_length,sepal_width,petal_length,petal_width
-
Use all available columns as Predictors: No
These figures displays the results for the mentioned parameter settings for the demographics data set.
Components
Variance