Example 1 - Cox Proportional Hazards Model Survival
The data set for this example, HPAstaining.sta, is taken from Collett (2003). The data consists of survival times of breast cancer patients with tumors that were stained positively or negatively with a histochemical marker from the Roman snail known as Helix pomatia agglutinin or HPA.
Prerequisites
Open the example data file HPAstaining.sta, and start the Cox Proportional Hazards module. Following are instructions to do this from the ribbon bar and from the classic menus.
Procedure
-
To open a
Open a Statistica Data File dialog box:
- Ribbon bar: Select the
Home tab. In the
File group, click the Open arrow, and select
Open Examples to display the
Open a Statistica Data File dialog box. The data set is located in the Datasets folder.
Next, on the Statistics tab, in the Advanced/Multivariate group, click the Advanced Models arrow and select Cox Proportional Hazards to display the Cox Proportional Hazards Regression dialog box.
- Classic Menu: From the
File menu, select
Open Examples to display the
Open a Statistica Data File dialog box.
HPAstaining.sta is located in the
Datasets folder.
Next, from the Statistics - Advanced Linear/Nonlinear submenu, select Cox Proportional Hazards Models.
- Ribbon bar: Select the
Home tab. In the
File group, click the Open arrow, and select
Open Examples to display the
Open a Statistica Data File dialog box. The data set is located in the Datasets folder.
- Starting the analysis: On the Quick tab, in the Input type group box, ensure that the Survival time, covariates, factors, censor option button is selected.
- Click the Variables button to display the variable specification dialog box, and make the following variable selections.
- Click the OK button in the variable selection dialog box.
-
Specify the codes for the complete and censored values. Enter a value of 1 for a complete responses and a value of 0 for a censored responses.
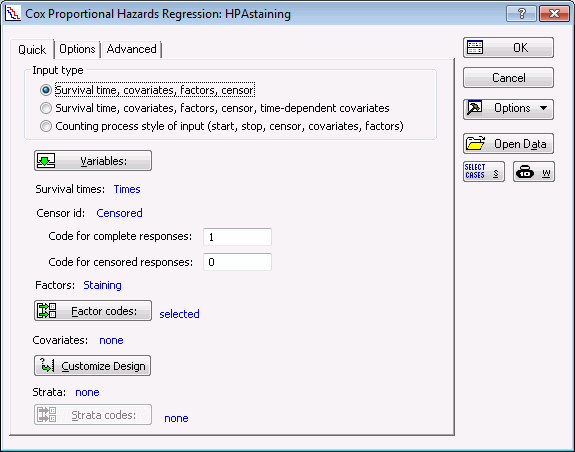
Staining is a categorical factor. Statistica provides options on how to code a categorical factor. To keep consistent with the example in Collett, we use the reference cell coding using the value of Negative as the reference; that is, the Positive value is recoded to a 1 and the Negative value are recoded to a 0.
- Select the Options tab. In the Coding of factors group box, select the Reference option button.
- Click the Set reference category button to display the Specify Codes dialog box.
- Click the Zoom button to display the Values/Stats dialog box, and select the value Negative.
- Click OK in the Values/Stats dialog box.
- Click OK in the Specify Codes dialog box.
- Click OK in the Cox Proportional Hazards Regression dialog box to run the analysis and display the Cox Proportional Hazards Results dialog box.
-
On the
Quick tab, click the
Parameter estimates button to create the following spreadsheet.

The parameter estimate is 0.908 with a standard error of approximately 0.501. Recall that the proportional hazards model assumes the following form of the hazard function:
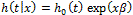
Since the value of Positive is assigned the value of 1 and Negative is assigned the value of 0, we can compute the following ratio of the hazard functions, that is, the hazard ratio, of the Positive and Negative stained tumors as follows:
Notice that this value is provided in the output already. The value is approximately 2.48. Since this is greater than 1, we can conclude that the woman with a positively stained tumor has an increased risk of death as compared to a woman with a negatively stained tumor.
We can see this more clearly by displaying the survivor functions for the two groups.
- In the Cox Proportional Hazards Results dialog box, select the Survivor Function tab. Specify the Number of covariate patterns as 2. Click the Specify covariate values button to display the Specify covariate values dialog box. Enter the values Positive and Negative for Case 1 and Case 2 respectively.
- Click the OK button.
- Since we are displaying 2 survival curves on 1 graph, in the Survivor function group box, clear the Add confidence interval check box.
- Click the Plot button.






