Boosted Trees for Regression and Classification Overview (Stochastic Gradient Boosting) - Basic Ideas
The Statistica Boosted Trees module is a full featured implementation of the stochastic gradient boosting method. The general computational approach is also known by the names TreeNet (TM Salford Systems, Inc.) and MART (TM Jerill, Inc.). Over the past few years, this technique has emerged as one of the most powerful methods for predictive data mining. The implementation of these powerful algorithms in Statistica Boosted Trees allows them to be used for regression as well as classification problems, with continuous and/or categorical predictors, and also provides options to deploy models for computing predictions or predicted classifications (scoring). Detailed technical descriptions of these methods can be found in Friedman (1999a, b) as well as Hastie, Tibshirani, & Friedman (2001; see also, Nisbet, R., Elder, J., & Miner, G. (2009) and Computational Details).
As with all statistical analysis facilities of Statistica, Statistica Data Miner, and Statistica Enterprise Server, these methods can be used in conjunction (or competition) with all other techniques for predictive data mining, as well as the various graphical techniques for evaluating models for regression and classification.
Gradient Boosting Trees
The algorithm for Boosted Trees evolved from the application of boosting methods to regression trees [see also General Classification and Regression Trees (GC&RT)]. The general idea is to compute a sequence of (very) simple trees, where each successive tree is built for the prediction residuals of the preceding tree. As described in the General Classification and Regression Trees Introductory Overview, this method will build binary trees, such as partitioning the data into two samples at each split node. Now suppose that you were to limit the complexities of the trees to 3 nodes only (actually, the complexity of the trees can be selected by the user): A root node and two child nodes, for instance, a single split. Thus, at each step of the boosting (boosting trees algorithm), a simple (best) partitioning of the data is determined, and the deviations of the observed values from the respective means (residuals for each partition) are computed. The next 3-node tree will then be fitted to those residuals, to find another partition that will further reduce the residual (error) variance for the data, given the preceding sequence of trees.
It can be shown that such additive weighted expansions of trees can eventually produce an excellent fit of the predicted values to the observed values, even if the specific nature of the relationships between the predictor variables and the dependent variable of interest is very complex (nonlinear in nature). Hence, the method of gradient boosting - fitting a weighted additive expansion of simple trees - represents a very general and powerful machine learning algorithm.
The Problem of Overfitting; Stochastic Gradient Boosting
One of the major problems of all machine learning algorithms is to know when to stop, for instance, how to prevent the learning algorithm to fit esoteric aspects of the training data that are not likely to improve the predictive validity of the respective model.
This issue is also known as the problem of overfitting. To reiterate, this is a general problem applicable to most machine learning algorithms used in predictive data mining (see, for example, Statistica Automated Neural Networks (SANN) or Multivariate Adaptive Regression Splines (MARSplines)).
A general solution to this problem, used for example in SANN, is to evaluate the quality of the fitted model by predicting observations in a test-sample of data that have not been used before to estimate the respective model(s). In this manner, one hopes to gage the predictive accuracy of the respective solution, and to detect when overfitting has occurred (or is starting to occur).
The solutions implemented in Statistica Boosted Trees take a similar approach. First, each consecutive simple tree is built for only a randomly selected subsample of the full data set. In other words, each consecutive tree is built for the prediction residuals (from all preceding trees) of an independently drawn random sample. The introduction of a certain degree of randomness into the analysis in this manner can serve as a powerful safeguard against overfitting (since each consecutive tree is built for a different sample of observations), and yield models (additive weighted expansions of simple trees) that generalize well to new observations, i.e., exhibit good predictive validity. This technique, i.e., performing consecutive boosting computations on independently drawn samples of observations, is knows as stochastic gradient boosting.
Second, the StatisticaBoosted Trees Results dialog box contains an option to plot not only the prediction error function for the training data over successive trees, but also for an independently sampled testing data.
With this graph, you can identify very quickly the point where the model (consisting of a certain number of successive trees) begins to overfit the data; see, for example, Example 1: Classification via Boosted Trees for details).
Stochastic Gradient Boosting Trees and Classification
So far, the discussion of boosting trees has exclusively focused on regression problems, i.e., on the prediction of a continuous dependent variable. The technique can easily be expanded to handle classification problems as well (this is described in detail in Friedman, 1999a, section 4.6; in particular, see Algorithm 6):
First, different boosting trees are built for (fitted to) each category or class of the categorical dependent variable, after creating a coded variable (vector) of values for each class with the values 1 or 0 to indicate whether or not an observation does or does not belong to the respective class. In successive boosting steps, the algorithm will apply the logistic transformation (see also Nonlinear Estimation) to compute the residuals for subsequent boosting steps. To compute the final classification probabilities, the logistic transformation is again applied to the predictions for each 0/1 coded vector (class). This algorithm is described in detail in Friedman (1999a; see also Hastie, Tibshirani, and Freedman, 2001, for a description of this general procedure).
Large numbers of categories
The computational effort generally becomes larger by a multiple of what it takes to solve a simple regression prediction problem (for a single continuous dependent variable). Therefore, it is not prudent to analyze categorical dependent variables (class variables) with more than, approximately, 100 or so classes; past that point, the computations performed by the program may require an unreasonable amount of effort and time. (For example, a problem with 200 boosting steps and 100 categories or classes for the dependent variable would yield 200 * 100 = 20,000 individual trees!)
Parameters for Stochastic Gradient Boosting
To summarize, the Statistica Boosted Trees module will compute a weighted additive expansion of simple regression trees, fitted to the prediction residuals computed based on all preceding trees.
In this procedure, each individual tree is fitted to the residuals computed for an independently drawn sample of observations, thereby introducing a certain degree of randomness into the estimation procedure that has been shown to avoid overfitting, and yield solutions with good predictive validity.
The following parameters can be set to control this algorithm:
Maximum number of nodes for each tree
First, you can determine the maximum number of nodes for each individual tree in the boosting sequence. In most applications, a very simple 3-node tree is sufficient, i.e., a single split or partitioning of the training sample at each step.
Number of additive terms
Next, you can determine the number of consecutive trees (additive terms) you want to compute.
For complex data analysis problems and relationships (between predictors and dependent variables), several hundred simple trees may be required to arrive at a good predictive model; for classification problems, that number must be multiplied by the number of categories or classes for the categorical dependent variable.
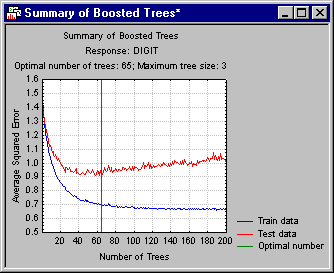
The Statistica Boosted Trees module also computes, for each additive term or step in the boosting sequence, the prediction error for a randomly selected (or determined by the user) testing sample. By plotting the prediction error for the training and testing sample over the successive boosted trees, an obvious point of overfitting can often be identified.

For example, consider the result shown here. Notice how the prediction error for the training data steadily decreases as more and more additive terms (trees) are added to the model.
However, somewhere past 35 trees, the performance for independently sampled testing data actually begins to deteriorate, clearly indicating the point where the model begins to overfit the data. Statistica Boosted Trees will automatically determine this point, and compute predicted values or classifications (and generate deployment code for computing predicted values or classifications; e.g., via Rapid Deployment of Models) for the respective number of trees.
Learning rate
As described above, the Statistica Boosted Trees module will compute a weighted additive expansion of simple regression trees (see also Computational Details).
The specific weight with which consecutive simple trees are added into the prediction equation is usually a constant, and referred to as the learning rate or shrinkage parameter. According to Friedman (1999b, p. 2; 1999a), empirical studies have shown that shrinkage values of .1 or less usually lead to better models (with better predictive validity). See Computational Details for more information.
Missing data
The implementation of the stochastic gradient boosting algorithm in Statistica can flexibly incorporate missing data in the predictors.
When, during model building, missing data are encountered for a particular observation (case), then the prediction for that case is made based on the last preceding (non-terminal) node in the respective tree. So, for example, if at a particular point in the sequence of trees a predictor variable is selected at the root (or other non-terminal) node for which some cases have no valid data, then the prediction for those cases is simply based on the overall mean at the root (or other non-terminal) node. Hence, there is no need to eliminate cases from the analysis if they have missing data for some of the predictors, nor is it necessary to compute surrogate split statistics (e.g., see also the documentation for the Number of surrogates option on the Interactive Trees Specifications dialog box - Advanced tab for C&RT).
Summary
The methods available in the Statistica Boosted Trees module provide a very powerful machine learning tool for predictive data mining.
The technique can approximate practically all types of nonlinear relationships between predictors and dependent variables, and often provides much quicker and simpler solutions than, for example, the various neural networks architectures available in Statistica Automated Neural Networks (SANN). The implementation of these techniques in Statistica are very general, and can be applied to regression and classification problems, with continuous and/or categorical predictors.