Advanced Example 6: Response Optimization
This example describes how to profile predicted responses and optimize the desirability of responses. For details concerning these methods, also refer to the Experimental Design module, Profiling Predicted Responses and Response Desirability (this example is also discussed there).
The procedures used in product development generally involve two steps: 1) predicting responses on the dependent, or Y variables, by fitting the observed characteristics of the product using a regression equation based on the levels of the independent, or X variables, and 2) finding the levels of the X variables that simultaneously produce the most desirable predicted responses on the Y variables. Derringer and Suich (1980) give, as an example of these procedures, the problem of finding the most desirable tire tread compound. In their example, there are four Y variables: PICO Abrasion Index, 200 percent modulus, elongation at break, and hardness. The characteristics of the product in terms of the response variables depend on the ingredients, the X variables: hydrated silica level, silane coupling level, and sulfur. The problem is to find the levels of the ingredients that produce the most desirable tire tread compound in terms of the four outcome measures.
- Specifying the analysis
- Derringer and Suich (1980) used a central composite (response surface) design to investigate the effects of the tire tread ingredients on the desirability of the product. The data for the completed experiment of 20 runs (as listed on p. 217 of Derringer & Suich, 1980) are contained in the example data file Tiretre.sta.
Ribbon bar. Select the Home tab. In the File group, click the Open arrow and select Open Examples to display the Open a STATISTICA Data File dialog box. The Tiretre.sta data file is located in the Datasets folder. Then, select the Statistics tab. In the Advanced/Multivariate group, click Advanced Models and from the menu, select General Linear to display the General Linear Models (GLM) Startup Panel.
Classic menus. On the File menu, select Open Examples to display the Open a STATISTICA Data File dialog box. The Tiretre.sta data file is located in the Datasets folder. Next, from the Statistics - Advanced Linear/Nonlinear Models submenu, select General Linear Models to display the General Linear Models (GLM) Startup Panel.
Select Response surface regression as the Type of analysis and Quick specs dialog as the Specification method. Click the OK button to display the GLM Response Surface Regression Quick Specs dialog box.
On the Quick tab, click the Variables button to display a standard variable selection dialog box. Specify Abrasion, Modulus, Elong, and Hardness, as the Dependent variables, and Silica, Silane, and Sulfur as the Continuous pred. variables. Click the OK button.
The design is a standard, three-variable, rotatable, central composite design with six center points. Derringer and Suich (1980) fitted responses on the dependent variables to a second degree polynomial, response surface model.
In the GLM Response Surface Regression dialog box, click the OK button to perform the analysis and display the GLM Results dialog box. The resulting regression equation is used in computing predicted values for the dependent variables at different combinations of levels of the independent variables. To profile the predicted responses and the desirability of responses, select the Profiler tab to reveal the options for desirability profiling.
Response/Desirability Profiling.
- Specifying desirability functions
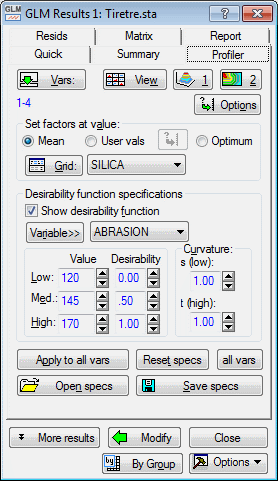
- Because we want to profile both the predicted responses on the dependent variables as well as the overall response desirability, the first step is to specify the desirability function for each dependent variable. To do this, select the Show desirability function check box to enable the edit fields for the Desirability function specifications.
Note: the first dependent variable, Abrasion, is displayed in the Variable box, indicating that the Desirability function specifications you specify will be applied to predicted values for Abrasion. Derringer and Suich (1980) specified the desirability function for Abrasion by assigning desirability values of 0.0 (for undesirable) to predicted values of Abrasion below 120, desirability values of 1.0 (for very desirable) to predicted values of Abrasion above 170, and linearly increasing desirability values between 0.0 and 1.0 for predicted values of Abrasion between 120 and 170. This desirability function for Abrasion is specified by entering the values of 120, 145 (the midpoint value), and 170 in the Low Value, Med. Value, and High Value fields, respectively, indicating that these predicted values correspond to the three "inflection" points in the desirability function for Abrasion.
The corresponding default Desirability values of 0.00, .50, and 1.00 are preset in the Low Desirability, Med. desirability, and High desirability fields, respectively. Because the function does not specify any curvature in the "fall off" of desirability between inflection points, the values in the s (low) parameter and t (high) parameter fields can be left at their default values of 1.00, specifying linear changes in desirability between inflection points.
The same procedure is followed for specifying the desirability functions for the remaining three dependent variables: select the dependent variable for which to supply desirability function specifications in the Variable box, and then enter the specifications in the appropriate field. Derringer and Suich's (1980) specifications for the remaining three dependent variables are shown below.
- Profiling the predicted responses and response desirability
- Click the View button to produce a compound response profile graph, using the factor means as the default current values for each predictor variable, and 4 steps from the observed minimum to the observed maximum to define the default 5 grid points for each factor. A prediction profile for each dependent variable is shown, consisting of a series of graphs, one for each independent variable, of the predicted values for the dependent variable at each grid point of the independent variable, holding the levels of all other independent variables constant at their current values. By default, confidence intervals for the predicted values are also shown.
Graphs of the desirability functions for each dependent variable are displayed, and a series of graphs, one for each independent variable, shows the profile of overall response desirability at each grid point of the independent variable, holding the levels of all other independent variables constant at their current values. The overall desirability value of .17956 indicates that the mean values of the tire tread ingredients do not yield a very desirable tire tread compound, but the profile of overall response desirability also shows that a level of Sulfur lower than its mean could produce a more desirable product.
A search for the levels of the ingredients that produce the most desirable product can be conducted. This is specified by selecting the Optimum option button in the Set factors at value group box.
Also, to display finer grids of predicted values and overall response desirability scores, click the Grid button to display the Specifications for factor grid dialog box, and enter 20 for the No. of steps. Click the accompanying Apply to all button to specify a grid of 21 points for each independent variable. Click the OK button to return to the Profiler tab.
Click the View button to produce a compound response profile graph, using the optimal values of the independent variables as their current values, and 20 steps from the observed minimum to the observed maximum to define the 21 grid points for each factor.
The results displayed on the compound response profile graph show that desirability is improved by setting the factors at levels other than their means. The overall desirability value is .581 with the settings of Silica, Silane, and Sulfur at .000, .168, and -.838, respectively. Derringer and Suich (1980) reported an overall desirability of .583 with the settings of Silica, Silane, and Sulfur at -.050, .145, and -.868, respectively, using a FORTRAN search program only briefly described in their article.
Surface plots and contour plots for overall response desirability can be produced via the Profiler tab. These plots are useful for interpreting the effects on overall response desirability of different combinations of levels of each pair of independent variables, with the remaining independent variables held constant at their current values. Click the Surface plot 1 button to produce a compound graph with three 3-D surface plots in which pairs of independent variables are represented on two of the axes and overall response desirability is represented on the third axis.
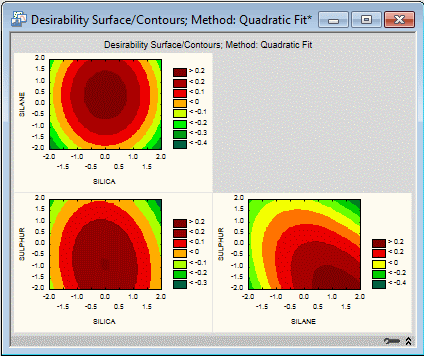
Click the Contour plot 2 button to produce a compound graph with three contour plots showing the levels of overall response desirability produced in different regions of the plane defined by pairs of independent variables, where each region of the plane represents a different combination of the levels of the two variables.
All of these plots show that the surface is relatively flat near the maximum, meaning that small departures from the optimal settings for the independent variables would not appreciably decrease the desirability of the product. More generally, these graphic features can aid in distinguishing between factors that are "inert" and "active" with respect to other factors. For "inert" ingredients, the desirability surface or contours are "flat" with respect to an "inert" ingredient's axis. The desirability surface or contours change at different levels of an "active" ingredient.
- Summary
- This example has shown how to simultaneously optimize several response variables in a central composite design. The same general procedures are used to find the levels of the predictor variables that optimize overall response desirability in other types of designs: 1) fit the observed characteristics of the product using an appropriate prediction equation based on the levels of the factors, and 2) find the levels of the factors that simultaneously produce the most desirable predicted characteristics of the product. GLM''s analysis options help to accomplish the first step, and the
Profiler tab options are useful for carrying out the important second step in the process of product development.
See also GLM - Index.