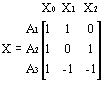GLM Introductory Overview - Separate Slope Designs
The traditional analysis of covariance (ANCOVA) design for categorical and continuous predictor variables is inappropriate when the categorical and continuous predictors interact in influencing responses on the outcome. The appropriate design for modeling the influences of the predictors in this situation is called the separate slope design. For the same example data used to illustrate traditional ANCOVA, the overparameterized X matrix for the design that includes the main effect of the three-level categorical predictor A and the 2-way interaction of P by A would be
The b4, b5, and b6 coefficients in the regression equation
Y = b0 + b1X1 + b2X2 + b3X3 + b4X4 + b5X5 + b6X6
give the separate slopes for the regression of the outcome on P within each group on A, controlling for the main effect of A.
As with nested ANOVA designs, the sigma-restricted coding of effects for separate slope designs is overly restrictive, so only the overparameterized model is used to represent separate slope designs. In fact, separate slope designs are identical in form to nested ANOVA designs, since the main effects for continuous predictors are omitted in separate slope designs.
Between-subject designs
Within-subject (repeated measures) designs
Multivariate designs