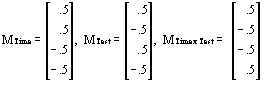GLM Introductory Overview - Multi-Way Within-Subject Designs
Suppose that in the example algebra skills study with the Time repeated measures factor (see the Within-Subject Designs Overview), students were given a number problem test and then a word problem test on each testing occasion. Test could then be considered as a second repeated measures factor, with scores on the number problem tests representing responses at level 1 of the Test repeated measure factor, and scores on the word problem tests representing responses at level 2 of the Test repeated measure factor. The within subject design for the study would be a 2 (Time) by 2 (Test) full-factorial design, with effects for Time, Test, and the Time by Test interaction.
To construct transformed dependent variables representing the effects of Time, Test, and the Time by Test interaction, three respective M transformations of the original dependent Y variables are performed. Assuming that the original Y variables are in the order Time 1 - Test 1, Time 1 - Test 2, Time 2 - Test 1, and Time 2 - Test 2, the M matrices for the Time, Test, and the Time by Test interaction would be
The differences of the mean scores on the transformed T variables from 0 are then used to interpret the corresponding within-subject effects. If the b0 coefficient in the regression of a transformed T variable on the intercept is non-zero, this indicates a change in responses across the levels of a repeated measures effect, that is, the presence of the corresponding main or interaction effect for the repeated measure factors on responses.
Interpretation of within by between interaction effects follow the same procedures as for one-way within designs, except that now within by between interactions are examined for each within effect by between effect combination.
Between-subject designs
Within-subject (repeated measures) designs
Multivariate designs