Z Benchmark Potential
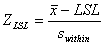
Where
| ZLSL | = | Z benchmark LSL |
| LSL | = | Lower Specification Limit |
| = | Sample mean | |
| swithin | = | Sigma within estimate |

Where
| ZUSL | = | Z benchmark LSL |
| USL | = | Upper Specification Limit |
| = | Sample mean | |
| swithin | = | Sigma within estimate |

Where
| ZPotential | = | Z benchmark Potential |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |
| Φ-1 | = | Inverse Standard Normal distribution function |
| Φ | = | Cumulative Standard Normal distribution function |
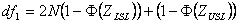
Where
| df1 | = | Numerator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |

Where
| df2 | = | Denominator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |
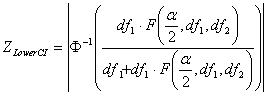
Where
| ZLowerCI | = | Z benchmark Lower CI |
| Φ-1 | = | Inverse Standard Normal distribution function |
| = | Value from F(df1,df2) distribution with area of α in right tail |
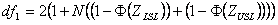
Where
| df1 | = | Numerator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |
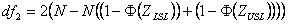
Where
| df2 | = | Denominator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |
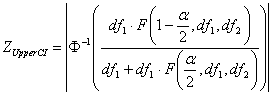
Where
| ZUpperCI | = | Z benchmark Upper CI |
| Φ-1 | = | Inverse Standard Normal distribution function |
| = | Value from F(df1,df2) distribution with area of α in right tail |
Table for Function(n)
| n | Function(n) |
| Using Ranges: | |
| All n |
|
| Using Sample Standard Deviation: | |
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6-7 |
|
| 8-9 |
|
| 10-17 |
|
| 18-64 |
|
| >64 | 1 |
10.
Where
| Function(n) | = | Value from table above |
| n | = | Average sample size |
| k | = | Number of samples |
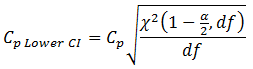
Where
| Cp LowerCI | = | Cp Lower CI |
| Cp | = | Potential Capability |
| χ2 (α,df) | = | Value from χ2 (df) distribution with area of α in right tail |

Where
| Cp UpperCI | = | Cp Upper CI |
| Cp | = | Potential Capability |
| χ2 (α,df) | = | Value from χ2 (df) distribution with area of α in right tail |

Where
| Cpk LowerCI | = | Cpk Lower CI |
| Cpk | = | Demonstrated Excellence |
| Φ-1 | = | Inverse Standard Normal distribution function |
| k | = | Number of samples |
| n | = | Average sample size |
14.
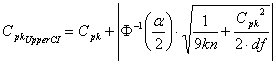
Where
| Cpk UpperCI | = | Cpk Upper CI |
| Cpk | = | Demonstrated Excellence |
| Φ-1 | = | Inverse Standard Normal distribution function |
| k | = | Number of samples |
| n | = | Average sample size |
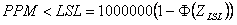
Where
| PPM<LSL | = | Parts per million less than LSL |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
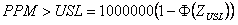
Where
| PPM>USL | = | Parts per million less greater than USL |
| Φ | = | Cumulative Standard Normal distribution function |
| ZUSL | = | Z benchmark Upper Specification Limit |

Where PPMTotal = Total Parts per million
Observed Process Performance:

Where
| PPM<LSL | = | Parts per million less than LSL |
| LSL | = | Lower Specification Limit |
| N | = | Total number of observations |
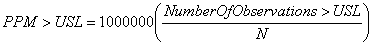
Where
| PPM>USL | = | Parts per million greater than USL |
| USL | = | Upper Specification Limit |
| N | = | Total number of observations |
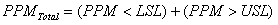
Where PPMTotal = Total Parts per million

Where
| = | Sample mean | |
| soverall | = | Estimate of overall sigma |
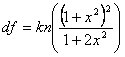
Where
| df | = | Degrees of freedom for χ2 distribution |
| k | = | Number of samples |
| n | = | Average sample size |
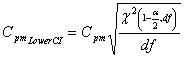
Where
| Cpm LowerCI | = | Cpm Lower CI |
| Cpm | = | Potential Capability II |
| χ2 (α,df) | = | Value from χ2 (df) distribution with area of α in right tail |
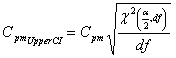
Where
| Cpm UpperCI | = | Cpm Upper CI |
| Cpm | = | Potential Capability II |
| χ2 (α,df) | = | Value from χ2 (df) distribution with area of α in right tail |
Computation for Z Benchmark overall:
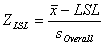
Where
| ZLSL | = | Z benchmark LSL |
| LSL | = | Lower Specification Limit |
| = | Sample mean | |
| soverall | = | Sigma overall estimate |

Where
| ZUSL | = | Z benchmark USL |
| USL | = | Upper Specification Limit |
| = | Sample mean | |
| soverall | = | Sigma overall estimate |
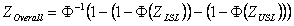
Where
| ZOverall | = | Z benchmark Overall |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |
| Φ-1 | = | Inverse Standard Normal distribution function |
| Φ | = | Cumulative Standard Normal distribution function |

Where
| df1 | = | Numerator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |

Where
| df2 | = | Denominator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |
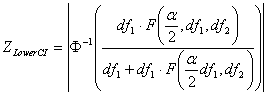
Where
| ZLowerCI | = | Z benchmark Lower CI |
| Φ-1 | = | Inverse Standard Normal distribution function |
| = | Value from F(df1,df2) distribution with area of α in right tail |

Where
| df1 | = | Numerator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |

Where
| df2 | = | Denominator degrees of freedom for F distribution |
| N | = | Total number of observations |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
| ZUSL | = | Z benchmark Upper Specification Limit |

Where
| ZUpperCI | = | Z benchmark Upper CI |
| Φ-1 | = | Inverse Standard Normal distribution function |
| = | Value from F(df1,df2) distribution with area of α in right tail |
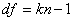
Where
| df | = | Degrees of freedom for χ2 distribution |
| k | = | Number of samples |
| n | = | Average sample size |

Where
| P p LowerCI | = | Pp Lower CI |
| Pp | = | Performance Index |
| χ2 (α,df) | = | Value from χ2 (df) distribution with area of α in right tail |
36.

Where
| P p UpperCI | = | Pp Upper CI |
| Pp | = | Performance Index |
| χ2 (α,df) | = | Value from χ2 (df) distribution with area of α in right tail |

Where
| Ppk LowerCI | = | Ppk Lower CI |
| Ppk | = | Performance Demonstrated Excellence |
| Φ-1 | = | Inverse Standard Normal distribution function |
| k | = | Number of samples |
| n | = | Average sample size |

Where
| Ppk UpperCI | = | Ppk Upper CI |
| Ppk | = | Performance Demonstrated Excellence |
| Φ-1 | = | Inverse Standard Normal distribution function |
| k | = | Number of samples |
| n | = | Average sample size |
Potential Process Performance:

Where
| PPM<LSL | = | Parts per million less than LSL |
| Φ | = | Cumulative Standard Normal distribution function |
| ZLSL | = | Z benchmark Lower Specification Limit |
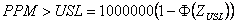
Where
| PPM>LSL | = | Parts per million greater than LSL |
| Φ | = | Cumulative Standard Normal distribution function |
| ZUSL | = | Z benchmark Upper Specification Limit |
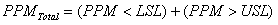
Where PPMTotal = Total Parts per million
Copyright © 2021. Cloud Software Group, Inc. All Rights Reserved.
