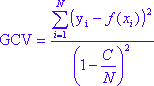Technical Notes: The Multivariate Adaptive Regression Splines (MARSplines) Model

These serve as basis functions for linear or nonlinear expansion that approximates some true underlying function f(x).

The MARSplines model for a dependent (outcome) variable y, and M terms, can be summarized in the following equation:

where the summation is over the M terms in the model, and bo and bm are parameters of the model (along with the knots t for each basis function, which are also estimated from the data). Function H is defined as:

where xv(k,m) is the predictor in the k'th of the m'th product. For order of interactions K=1 the model is additive, and for K=2 the model pairwise interactive.

During forward stepwise, a number of basis functions are added to the model according to a pre-determined maximum that should be considerably larger (twice as much at least) than the optimal (best least-squares fit).

After implementing the forward stepwise selection of basis functions, a backward procedure is applied in which the model is pruned by removing those basis functions that are associated with the smallest increase in the (least squares) goodness-of-fit. A least squares error function (inverse of goodness-of-fit) is computed. The so-called Generalized Cross Validation error is a measure of the goodness of fit that takes into account not only the residual error but also the model complexity as well. It is given by

with

where N is the number of cases in the data set, d is the effective degrees of freedom, which is equal to the number of independent basis functions. The quantity c is the penalty for adding a basis function. Experiments have shown that the best value for C can be found somewhere in the range 2 < d < 3 (see Hastie et al., 2001).