Categorized Graphs
One of the most important, general, and also powerful analytic methods involves dividing (splitting) the data set into categories in order to compare the patterns of data between the resulting subsets. This common technique is known under a variety of terms (such as breaking down, grouping, categorizing, splitting, slicing, drilling-down, or conditioning) and it is used both in exploratory data analyses and hypothesis testing. For example: A positive relation between the age and the risk of a heart attack may be different in males and females (it may be stronger in males). A promising relation between taking a drug and a decrease of the cholesterol level may be present only in women with a low blood pressure and only in their thirties and forties. The process capability indices or capability histograms can be different for periods of time supervised by different operators. The regression slopes can be different in different experimental groups.
There are many computational techniques that capitalize on grouping and that are designed to quantify the differences that the grouping will reveal (e.g., ANOVA/MANOVA). However, graphical techniques (such as categorized graphs discussed in this section) offer unique advantages that cannot be substituted by any computational method alone: they can reveal patterns that cannot be easily quantified (e.g., complex interactions, exceptions, anomalies) and they provide unique, multidimensional, global analytic perspectives to explore or "mine" the data.
What are Categorized Graphs? Categorized graphs (the term first used in Statistica software in 1990; also recently called Trellis graphs, by Becker, Cleveland, and Clark, at Bell Labs) produce a series of 2D, 3D, ternary, or nD graphs (such as histograms, scatterplots, line plots, surface plots, ternary scatterplots, etc.), one for each selected category of cases (i.e., subset of cases), for example, respondents from New York, Chicago, Dallas, etc. These component graphs are placed sequentially in one display, allowing for comparisons between the patterns of data shown in graphs for each of the requested groups (e.g., cities).
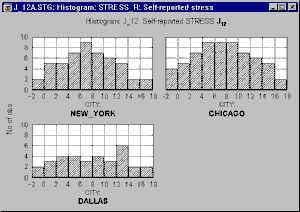
A variety of methods can be used to select the subsets; the simplest of them is using a categorical variable (e.g., a variable City, with three values New York, Chicago, and Dallas). For example, the following graph shows histograms of a variable representing self-reported stress levels in each of the three cities.
One could conclude that the data suggest that people who live in Dallas are less likely to report being stressed, while the patterns (distributions) of stress reporting in New York and Chicago are quite similar.
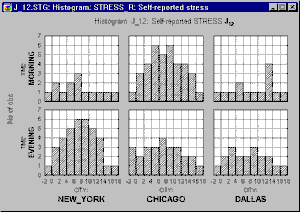
Categorized graphs in Statistica also support two-way or multi-way categorizations, where not one criterion (e.g., City) but two or more criteria (e.g., City and Time of the day) are used to create the subsets. Two-way categorized graphs can be thought of as "crosstabulations of graphs" where each component graph represents a cross-section of one level of one grouping variable (e.g., City) and one level of the other grouping variable (e.g., Time).
Adding this second factor reveals that the patterns of stress reporting in New York and Chicago are actually quite different when the Time of questioning is taken into consideration, whereas the Time factor makes little difference in Dallas.
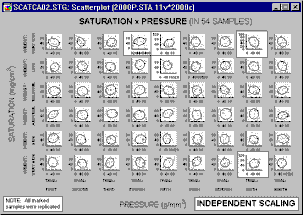
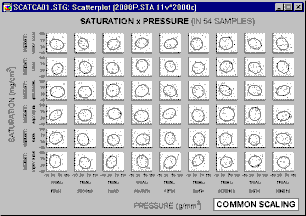
or all graphs can be scaled to a common scale wide enough to accommodate all values in all of the category graphs.
Common scaling allows the analyst to make comparisons of ranges and distributions of values among categories. However, if the ranges of values in graph categories are considerably different (causing a very wide common scale), then some of the graphs may be difficult to examine. The use of independent scaling may make it easier to spot trends and specific patterns within categories, but it may be more difficult to make comparisons of ranges of values among categories.