Sequence, Association, & Link Analysis (SAL) Technical Notes

The usefulness of this technique to address unique data mining problems is best illustrated in a simple example. Suppose you are collecting data at a check-out cash register in a large book store. Each customer transaction is logged in a database, and consists of the titles of the books purchased by the customer, magazine titles, gift items, etc. Hence, each record in the database will represent one customer (transaction), and may consist of a single book purchased by that customer or may consist of many different items (perhaps hundreds) that were purchased, arranged in an arbitrary order depending on the order in which the different items came down the conveyor belt at the cash register.

The purpose of the analysis is to find associations between the items that were purchased, i.e., to derive association rules that identify the items and co-occurrences of different items that appear with greatest frequencies. For example, you want to learn which books are likely to be purchased by a customer who you know already purchased (or is about to purchase) a particular title. This type of information could then quickly be used to suggest to the customer those additional titles. You may already be familiar with the results of these types of analyses if you are a customer of various online (Web-based) retail businesses; many times when making a purchase online, the vendor will suggest similar items at the time of "check-out," based on rules such as "customers who buy book title A are also likely to purchase book title B," and so on.

Similar to association rules, sequence rules are concerned with detecting the purchase of items in time. In other words, if item A was purchased at this point in time, what other items are likely to be bought by the same customer later on. If A was, for example, an electrical appliance or a new car, then it is likely that the buyer will be interested in an extended warranty shortly thereafter. Thus, in sequence analysis we are interested in detecting rules that can be defined over a sequence of transactions.

Link analysis is concerned with identification of relationships between various items in a data set. The techniques used to discover such rules are Association and Sequence analysis (see the Sequence, Association and Link Analysis Overview for further details).

In principle, Statistica already contains all the tools necessary to analyze data as described above, and to compute the results (tables) of interest. For example, Crosstabulation tables, and in particular Multiple Response tables in Basic Statistics can be used to analyze data of this kind (see the Technical Note on Coding of Multiple Response Variables). However, in cases when the number of different items in the data is very large (and not known ahead of time), and when the "factorial degree" of important rules is not known ahead of time, then the Basic Statistics tabulation facilities may be too cumbersome to use, or simply not applicable: Consider once more the simple bookstore example. First, the number of book titles is practically unlimited. In other words, if we made a table where each book title would represent one dimension, and the purchase of that book (yes/no) would be the classes or categories for each dimension, then the complete crosstabulation table would be huge and sparse (consisting mostly of empty cells). Alternatively, we could construct all possible two-way tables from all items available in the store; this would enable us to detect two-way rules between items. However, the number of tables that would have to be constructed would again be huge, most of the two-way tables would be sparse, and worse, if there were any three-way rules "hiding" in the data, we would miss them completely. The unique algorithm implemented in Sequence, Association and Link Analysis is capable of automatically detecting the relationships that are important without any significant effort from the user.

To summarize, you can use the Sequence, Association and Link Analysis module of Statistica to find rules of the kind If X then (likely) Y where X and Y can be single values, items, words, etc., or conjunctions of values, items, words, etc. [e.g., if (Car=Porsche and Gender=Male and Age<20) then (Risk=High and Insurance=High)]. The program can be used to analyze simple dichotomous variables and/or multiple response variables. Also possible is the use of continuous variables, which are divided into segments for rule extraction. The algorithm will determine the rules (association and/or sequence) without requiring the user to specify the number of distinct categories present in the data, or any prior knowledge regarding the maximum factorial degree or complexity of the important rules. Hence, this technique is particularly well suited for data and text mining of huge databases.

Computational Procedures and Terminology

Sequence, Association and Link Analysis is an implementation of a unique and fast algorithm that uses the powerful a priori algorithm (see Agrawal and Swami, 1993; Agrawal and Srikant, 1994; Han and Lakshmanan, 2001; see also Witten and Frank, 2000) together with a tree structured procedure that only requires one pass through data. Hence, it is fast and efficient and is particularly suitable for huge data sets for which other methods can be extremely slow.

Sequence, Association and Link Analysis supports all common types of variables or formats in which categories, items, or transactions (e.g., information regarding purchases of consumer items) are typically recorded.

Multiple response variables usually consist of multiple variables (i.e., a list of variables) that can contain, for each observation, codes or text values describing a single "dimension" or transaction. A good example of a multiple response variable is the case where a vendor records the purchases made by a customer in a single record, where each record could contain one or more items purchased, in arbitrary order. This is a typical format in which customer transaction data is kept. This type of data format is also discussed in great detail in the documentation for Basic Statistics (see Multiple Responses/Dichotomies - Multiple Response Variables).

In this data format, each variable would represent one item or category, and the dichotomous data in each variable would indicate whether the respective item or category applies to the respective case. For example, suppose a vendor creates a data spreadsheet where each column represents one of the products available for purchase. Each transaction (row of the data spreadsheet) records whether the respective customer did or did not purchase that product, i.e., whether the respective transaction involved each item. This type of data format is also discussed in great detail in the documentation for Basic Statistics (see Multiple Responses/Dichotomies - Multiple Response Variables).

Supporting continuous variables is one of the unique features of Sequence, Association and Link Analysis, which allows the inclusion of numeric variables for rule extraction. For example, a data set might record customer age together with the purchased items. A market analyst might then be interested in finding rules between specific items and age range of the customers. To this end, Sequence, Association and Link Analysis will divide the age variable into intervals and seek to find rules such as, if "A" then likely "Age Range".

The SAL algorithm attempts to derive from the data association rules of the form: If "Body" then "Head," where Body and Head stand for simple codes or text values (items), or the conjunction of codes and text values (items; e.g., if (Car=Porsche and Age<20) then (Risk=High and Insurance=High); here the logical conjunction before the then would be the Body, and the logical conjunction following the then would be the Head of the association rule).

Consider a set of 4 transactions each consisting of a number of items purchased by customers (shown in the table below).

Transactions	Items Bought
1	A, B, D
2	A, C
3	A, E
4	B, E, F

From the table of transactions shown above, we can drive a list of frequencies for the itemsets (an itemset contains one or more items).

Itemsets	Frequency
(A)	3
(B)	2
(C)	1
(D)	1
(E)	2
(F)	1
(A, B)	1
(A, C)	1

The frequency of an itemset is defined as the relative frequency of transactions containing that particular itemset, either as a whole or as a subset. The itemset (A), for example, occurs in transactions 1, 2, and 3. Thus, its relative frequency is 3. Similarly, the itemset (B) has a frequency of 2. The itemset (A, C) has the lowest frequency, 1. More complex itemsets such (A, B, C, F) do not occur (in this example). This is because, as a general rule, the more complex the itemset is (i.e., the larger the number of items it contains), the less likely to occur. In other words, complicated rules (see If Body then Head above) are harder to observe.

The support for an itemset is simply given by proportion of records in the transactions data set that have the itemset. Thus, for the itemset (A) we can write:

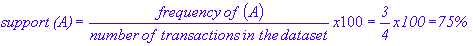
Similarly, we can calculate the support value for the rule "if A then C", (A, C) as:

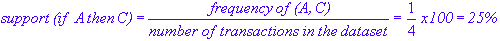
Thus, support is the probability that transactions containing A will also contain C. On the other hand, the confidence is defined as:

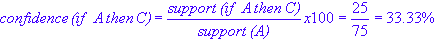
which is simply the conditional probability of transactions containing A will also contain C. Being a conditional probability, the confidence for "if A then C" is not  necessarily the same as the confidence for "if C then A."

The support and confidence are then combined to define lift for a rule. For example, the lift value for if A then C is given by: