Example 10.2: Constructing a Design from Vertex and Centroid Points (Example 9.1, Continued)
(1) xA - 2*xB ≥ 0
(2) xA + xB - xC ≥ 0
Ribbon bar. Select the Home tab. In the File group, click the Open arrow and on the menu, select Open Examples to display the Open a Statistica Data File dialog. Open the Constrr.sta data file, which is located in the Datasets folder.
Classic menus. On the File menu, select Open Examples to display the Open a Statistica Data File dialog. Open the Constrr.sta data file, which is located in the Datasets folder.
Now, suppose that you want to select from these 22 points the 15 points that can extract the most amount of information about the dependent variable, given a second-order model (i.e., with linear factor main effects, quadratic effects, and two-way interactions).
Ribbon bar. Select the Statistics tab, and in the Industrial Statistics group, click DOE to display the Design & Analysis of Experiments Startup Panel.
Classic menus. On the Statistics - Industrial Statistics & Six Sigma submenu, select Experimental Design (DOE) to display the Design & Analysis of Experiments Startup Panel.
Select the Advanced tab, select D- and A- (T-) optimal algorithmic designs, and click the OK button to display the D- and A- Optimal Designs dialog.
As before, you need to enter a candidate list of points, that is, the list of points from which you want the program to construct the design.
Click the Variables button, and in the variable selection dialog, select all three variables in the file. Click the OK button.
Then, select the Model tab.
Select the Lin/quad main eff. + 2-ways option button to specify the second-order model.
Finally, on the Optimization methods tab, in the Optimization criterion group box, enter 15 into the Number of points in final design box.
Now you are ready to select an optimization method.
Now, on the Optimization methods tab, click the Sequential (Dykstra) button to display the Optimal Design Result: Response Surface dialog.
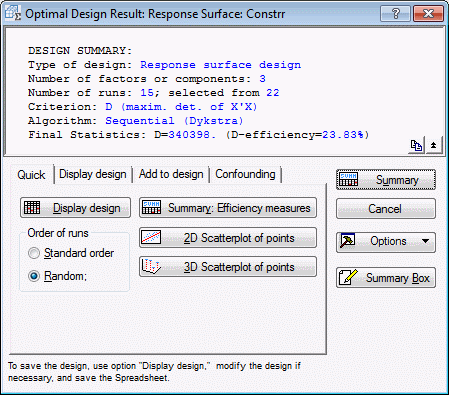
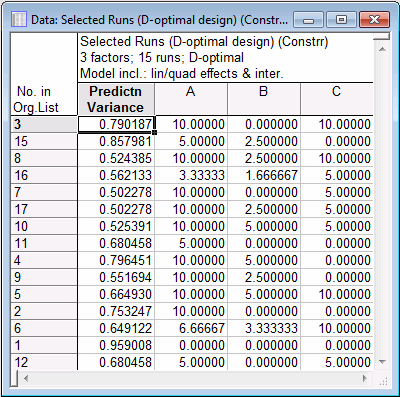
Return to the Optimal Design Result: Response Surface dialog, and click Cancel to return to the D- and A- Optimal Designs dialog. Then select the Options tab.
Here you have access to various technical parameters of the optimization process. These options are described in detail in the D- and A-Optimal Designs - Options tab topic.
First, in the Initial design group box, select the Select randomly option button. This will cause the program to choose the initial design by random from the candidate list [note that the Sequential (Dykstra) method does not require a design, and for that method, the setting of the options here is disregarded].
Then, click OK and try some of the other optimization techniques.
In most cases, you will get final selections of points that will be very similar to those generated by the Sequential (Dykstra) method; also, the D-efficiency measure will for most random trials be very similar in magnitude. Thus, we can conclude that the first design we reviewed is most likely not only locally optimal, but indeed the best (or close to the best) choice of design, given the candidate list, i.e., given the constrained nature of the experimental region.
See also, Experimental Design.