PCA Example

This example is based on the data file IndustrialEvaporator.sta. The data contains details of the process of drying a fixed quantity of a wet product placed in an evaporator bed. During the evaporation process, 8 variables - Dewpoint, Intake Temp, In-Process Air Temp, Exhaust Temp, Mass Air Flow, Bed Temp, Filter Pressure, and Bed Pressure - were measured between regular time intervals for monitoring and quality control.

Open the data file:

Ribbon bar. Select the Home tab. In the File group, click the Open arrow, and select Open Examples to display the Open a Statistica Data File dialog. IndustrialEvaporator.sta is located in the Datasets folder.

Classic menus. From the File menu, select Open Examples to display the Open a Statistica Data File dialog. IndustrialEvaporator.sta is located in the Datasets folder.

We will use Statistica Principal Components Analysis (PCA) to monitor and examine the evolution of the evaporation process of a wet product in order to detect abnormal conditions if they arise and to ensure the quality of the end product.

Start PCA:

Ribbon bar. Select the Statistics tab. Click Advanced Models, and from the menu, select NIPALS to display the PCA/PLS dialog.

Classic menus. From the Statistics - Advanced Linear/Nonlinear Models submenu, select NIPALS Algorithm (PCA/PLS) to display the PCA/PLS dialog.

Note that, alternatively, you can:

Ribbon bar. Select the Statistics tab. In the Advanced/Multivariate group, click PLS, PCA to display the

Multivariate Statistical Process Control

dialog.

Classic menus. From the Statistics menu, select PLS, PCA Multivariate/Batch SPC  to display the Multivariate Statistical Process Control dialog.

On the Quick tab of either dialog, select Principal component analysis (PCA) and click the OK button to display the PCA dialog. You can also double-click Principal component analysis (PCA) to display the dialog.

On the Quick tab, click the Variables button to display a variable selection dialog. Select variables 1 through 8 as the Continuous variables for the PCA analysis.

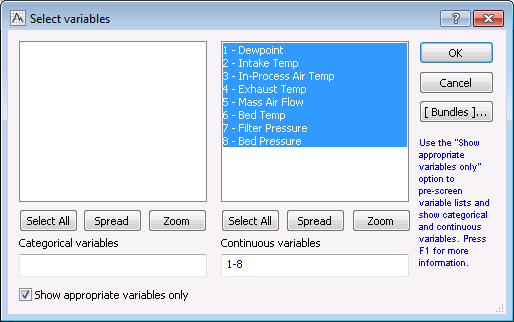
Click the OK button to close the variable selection dialog and return to the PCA dialog.

At this point you may want to check the analysis configuration, which is determined by the option settings on the Quick, NIPALS, Fitting, Options, and Advanced tabs. These tabs provide various options that may need to be reconfigured to suit your individual analysis.

For example, on the

NIPALS

tab, you can increase the Maximum number of iterations the NIPALS algorithm will be allowed to take for extracting a single component of the PCA model. You can also increase the accuracy for calculating the principal components by lowering the value of the Convergence criteria.

On the

Fitting

tab, you can select the method for determining the number of components in the PC (Principal Components) model. The number of principal components determines how complex your model will be. The more principal components a model has, the better it can fit the training data, at the expense of a less favorable performance on validation sets (i.e., poor generalization error). Thus, it is important that you select the number of components of your PC analysis with care. You can either let the cross-validation method determine this factor for you, or use the Fixed number of components option to set model complexity manually. Other options for determining model complexity include extracting all components with eigenvalues larger than a specified limit.

Although the seed for the cross-validation random number generator is determined by time on your computer, for this example, set its value to 1000 via the Seed option on the Fitting tab. This ensures that you reproduce the same results shown in the spreadsheets and graphs of this step-by-step example.

One of the important features of Statistica PCA is its preprocessing functionality, which enables you to scale data for better model building. The default setting is Unit standard deviations (this option is located on the

Advanced

tab), which should be suitable for most applications. Should this not be the case, however, you can provide your own scaling factors for the individual variables by selecting the User-defined standard deviations option button and then clicking the Define standard deviations button to display the User-defined scale (standard deviation) dialog where you can specify the scale. For this example, however, the default option (Unit standard deviations) is adequate.

The settings discussed above determine not only the results, but also the quality of your model, i.e., its ability to predict unseen examples and detect important features that might be present in the data set such as outliers. Detecting abnormalities (outliers) is one of the primary goals of process monitoring in quality control. Note that each analysis is unique, and care should be taken in configuring its settings.

Click the OK button in the PCA dialog. This will initiate the NIPALS algorithm (see NIPALS Overview and NIPALS Technical Notes). When complete, the PCA

Results

dialog is displayed.

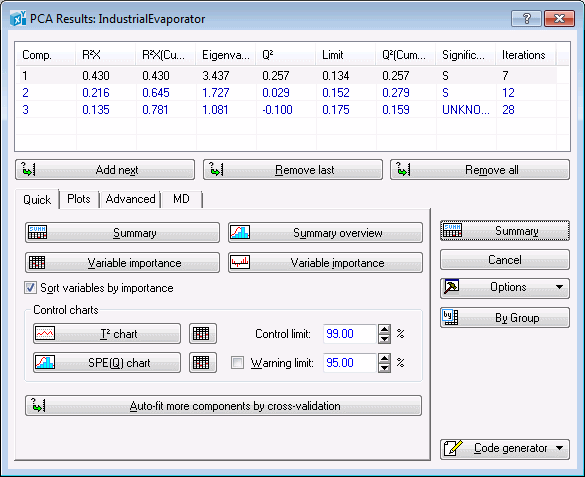
The Summary box is located at the top of the PCA Results dialog and contains information about the PC model such as R2X, Eigenvalues, Q2, Limit, Significance, and number of Iterations for each component. The same information can be displayed in a spreadsheet by clicking the Summary button.

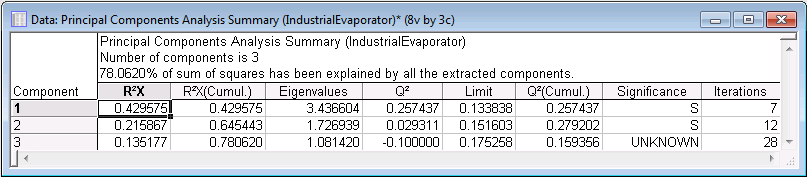
To generate histogram plots of the cumulative R2X and Q2, click the Summary overview button on the

Quick

tab.

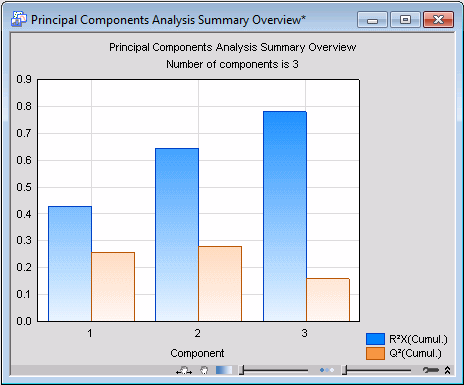
A study of the graph shows that cumulative R2X improves, i.e., tends to become unity, as more and more components are added to the PC model.

In this particular example, we used the cross-validation method for determining the optimal number of principal components (i.e., model complexity), which happens to be 3 in this case. This means that, on this occasion, the cross-validation algorithm found a PC model with 3 components to best represent the data set. See PCA and PLS Technical Notes for more details on cross-validation.

The variable importance is a useful quantity in PCA analysis. It measures how well a variable is represented by the principal components. This is often known as power, a quantity ranging from 0 to 1. For a mature model (i.e., a model with a sufficient number of components), variables that are not well represented (i.e., have low values of power) are more likely to be insignificant.

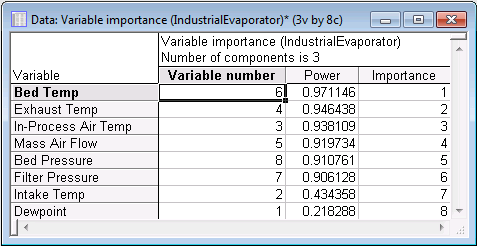
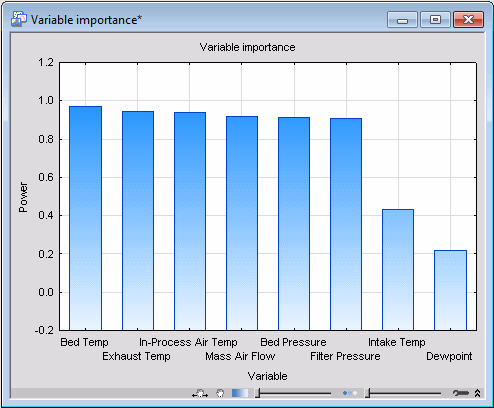
In order to display the variables in descending order in the spreadsheet, select the Sort variables by importance check box. Click the Variable importance button on the Quick tab to generate the variable importance spreadsheet.

Also, you can review the modeling power of the variables in histogram format by clicking the Variable importance button with the graph icon.

 .

The add and remove components feature can be used to monitor changes in importance of a variable with the increase in the number of principal components.

To do this, first click the Remove all button to remove all the components. Next, click (once) on the Add next button to add the first principal component.

Click the Variable importance graph button to generate a variable importance histogram.

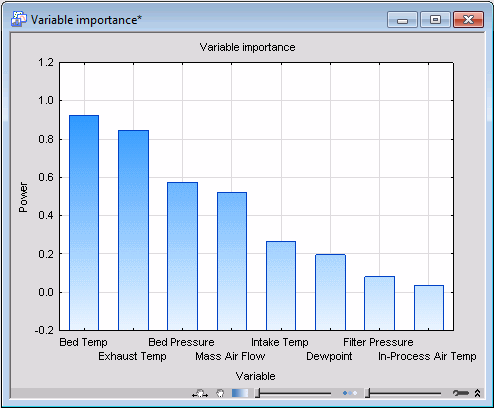
Examination of this graph shows that for this over-simplified model, i.e., a model lacking a sufficient number of principal components, most variables appear to be insignificant. This is because the model does not have enough components to sufficiently model the variables according to their true significance.

Keep adding more and more components to the model and print the corresponding importance histogram each time you add a dimension to the model.

Now examine the sequence of histograms you have generated. The first thing you should note is that the more components in the model, the larger the modeling power of the individual variables. In particular, note that variables Exhaust Temp and Bed Temp are predominantly modeled by PC1, while Filter Pressure is almost exclusively captured by PC2. This suggests that individual components model different individual variables (provided they are relevant).

Again, remove all the extracted components, and then click the Auto-fit more components by cross-validation button. This will recreate the initial PCA model that was built by clicking the OK button in the PCA dialog. In other words, it will take you back to that stage of the analysis before you manually removed and added components from and to the model.

So far we have analyzed the PC model to examine the variables. In other words, we have used the PC model for variable diagnostics by reviewing their significance. The PC model can also help you to analyze the data on a casewise basis by generating control charts that you can use to review and detect casewise abnormalities. This feature can be used for detecting outliers. For quality control purposes, outliers might be an indication of abnormal operating conditions that may affect the quality of the end product and, therefore, should be a cause for concern.

One important chart to review is the so-called Hotelling T2, which can be used to detect moderate (by comparison) outliers. Produce this chart by clicking the T2 chart button on the Quick tab.

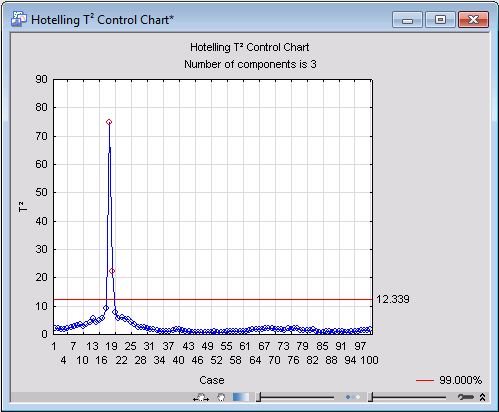
For this analysis, you can see that case 18 possesses a particularly a high value of T2 as compared to the rest of the observations. Case 19 also seems to be an outlier, although not as severe. Thus, we can conclude that at time intervals 18 and 19, the evaporation process was falling outside the scope of normality. The process, however, went back to normal after the elapse of those two time intervals, as values of T2 for the rest of the observations would indicate.

Another chart used to detect outliers is distance-to-model. This functionality is provided on the

Advanced

tab, where you can click any of the D-To-Model buttons to generate this information either in spreadsheet, line plot, or histogram formats (following is the line plot).

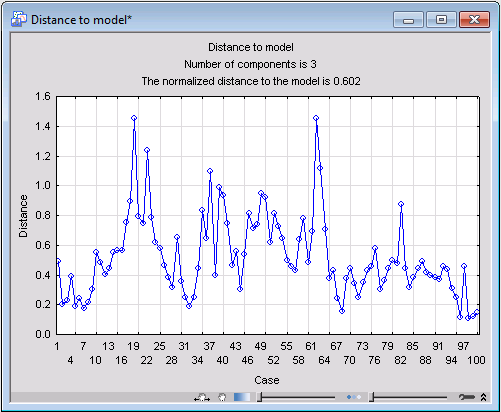
Case 62 shows up as an outlier in this graph, mostly likely because it has an outlying value on the variable Dewpoint (which is a weak predictor in terms of modeling power) of less than three standard deviations below the mean.

Further casewise data diagnostics can be carried out using the scatterplot of the x-scores. The x-scores are the transformed values of the X observations in the principal component system. An x-score with too high a value (i.e., one that deviates substantially from the point of origin) can again be regarded as an outlier or abnormal. To generate an x-scores scatterplot, select the

Plots

tab. In the First and Second component lists, select Component 1 and Component 2, respectively. In the Plot labels group box, select the Var/case name option button (to display variable names in the scatterplot).

Clear the Biplot check box, and click the Scatter (t) button to create a scatterplot of the x-scores for PC1 against the x-scores of PC2.

PCA can also help you to analyze the relationship between the original variables, the way they correlate to each other, and their influence in determining the new coordinate system. The quantity at the center of such analyses is the x-loadings factors. The x-loadings of a principal component with respect to a variable is the cosine of the angle between the directions of that component and the axis of the respective variable. This implies that the more influential a variable in determining a component, the more the variable axis is aligned with that component.

For the next step, we will generate a line plot of the x-loadings for PC1. Ensure that Component 1 is still selected in the First components list, and click the Lineplot (p) button to generate the line plot of the variables against the loadings of the first component.

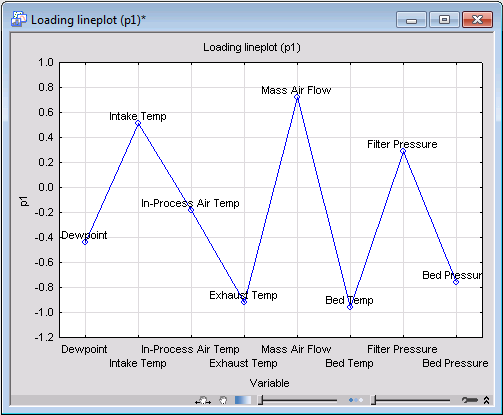
An examination of the plot shows that variable In-Process Air Temp is the least influential in determining the first principal component while Bed Temp plays the most significant important role. This conclusion is confirmed by the spreadsheet and histogram plots of the variables' importance (Variable importance button on the

Quick

tab) of the PCA model with one principal component, which shows that the respective variables have modeling powers 0.033526 and 0.921825. Note that you can generate the same graph for any principal component by making the appropriate selection in the First components list on the

Plots

tab.

Next, we will use scatterplots of the loading factors between various principal components to analyze the relation between the variables and identify the most influential ones in determining the PCA model.

Ensure that Component 1 and Component 2 are selected in the First and Second lists, respectively, on the Plots tab, and click the Scatter (p) button to create the scatterplot of the loading factors.

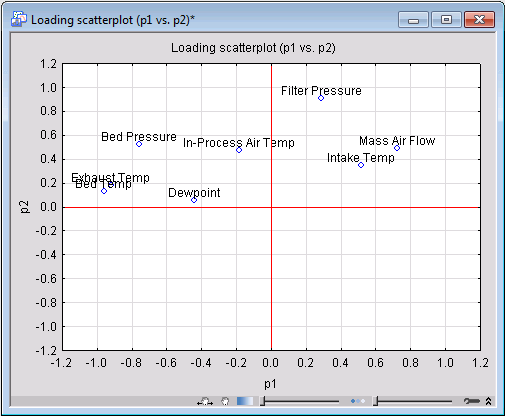
Study of this graph shows a noticeable amount of clustering among the variables. Variables placed close to each other influence the PCA model in similar ways, which also indicates they are correlated. Mass Air Flow and Intake Temp are examples of such variables with a substantial degree of correlation. In fact, the scatterplot of these two variables (which you can generate by clicking Scatterplot on the Statistica Graphs tab) show a nonlinear trend between the two.

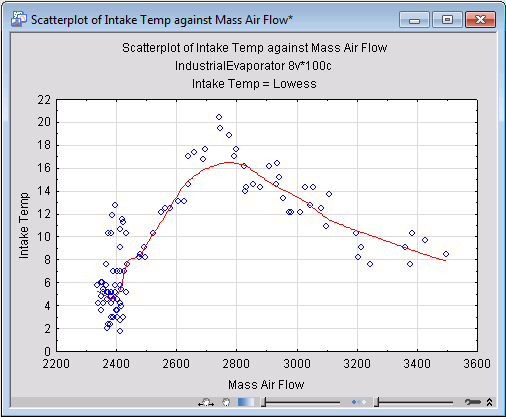
Other useful information in the loading scatterplot is the distance of its points from the origin. The further away a variable from the origin, the more influential the variable is in determining the PCA model.

As stated throughout this topic, the aim of PCA is to model a multivariate data set with the aid of a new coordinate system, known as the principal components, which is lesser in dimension than that of the original variables. This means, given a sufficient number of principal components, we can predict the original data set with a degree of accuracy that gets better and better, at least in principle, by adding more and more components into the model. However, since the aim here is to model the original data in lesser dimensions, there is always a difference (residuals) between the original observations and the predictions of the PC model.

On the

Advanced

tab, click the Residuals button to generate a spreadsheet of the residuals.

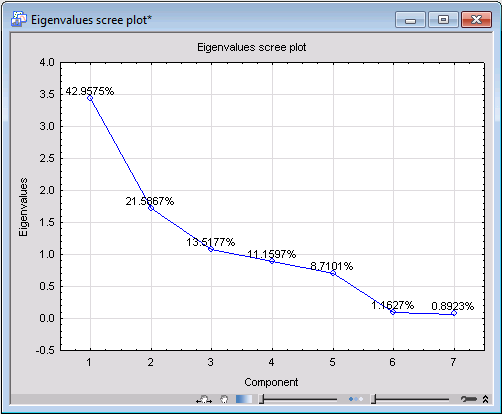
One of the fundamental quantities in PCA is the eigenvalues of the principal components, from which almost all properties of a PCA model can be derived. To generate the line plot of the principal eigenvalues, first select the number of the most significant components you want to display in the graph by adjusting the value of the Number of eigenvalues option on the

Advanced

tab. Set this value to 7 (the maximum number of components the current model can have is number of variables minus 1). Then, click the Scree plot button.

When the Principal Components Analysis is complete, often you need to save the model so you can use it later for deployment. With Statistica PCA, you can save your PC models in various formats including C\C++, Statistica Visual Basic, and PMML (Predictive Markup Model Language). To save a model, select one of the languages from the Code generator menu located in the

PCA Results

dialog, PMML for this example. This will output the model PMML code in a Statistica Report. Save the output with the extension .XML. Now your model is ready for deployment (see the PCA Deployment Example for more details).