NORMSDST および NORMSINV - 標準正規分布の計算
NORMSDST 関数と NORMSINV 関数は、標準正規分布曲線上で計算を実行します。NORMSDST 関数は、正規化値以下のデータ値の百分率を計算します。NORMSINV 関数は、NORMSDST 関数の逆で、標準正規分布曲線の百分位数の上限境界となる正規化値を計算します。
NORMSDST - 累積標準正規分布関数を計算
NORMSDST 関数は、標準正規分布上で計算を実行し、正規化値以下のデータ値の百分率を求めます。正規化数値は、標準正規分布曲線の平均値の標準偏差内の X 軸上の点です。正規分布データ内の百分位数を決定する際に役立ちます。
NORMSINV 関数は、NORMSDST の逆です。NORMSINV についての詳細は、NORMSDST および NORMSINV - 標準正規分布の計算を参照してください。
NORMSDST の結果は 6 桁の倍精度小数点数として返されます。
標準正規分布曲線は、平均値が 0 (ゼロ) で、標準偏差が 1 の正規分布です。この曲線下の領域の合計値は 1 です。標準正規分布の X 軸上の点は、「正規化数」と呼ばれます。データが正規分布されている場合、データ点を正規化数に変換することにより、ロースコア以下のスコアの百分率を得ることができます。
正規分布データの値 (ロースコア) を対応する正規化数 (z スコア) に変換するには、次の式を実行します。
z = (raw_score - mean)/standard_deviation
z スコアをロースコアに変換するには、次の式を使用します。
raw_score = z * standard_deviation + mean
データ点 xi (i は 1 から n) の平均値は、次のようになります。
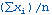
データ点 xi (i は 1 から n) の標準偏差は、次のようになります。

下図は、NORMSDST 関数と NORMSINV 関数の結果を示しています。
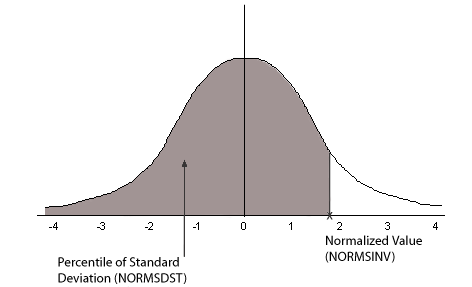
正規分布の特性
多くの一般的な測定は、正規分布です。データ値の正規分布は、釣鐘曲線になります。正規分布の作成には、平均値と標準偏差の 2 つの指標が必要です。
- 平均値は曲線の中心点です。
- 標準偏差は、平均値から変曲点 (曲線が方向を変更する点) までの距離で、曲線の広がりを示します。
累積標準正規分布関数を計算
NORMSDST(value, 'D8');
正規化された値です。
結果のフォーマットです。関数により返される値のフォーマットは倍精度小数点数です。有効な任意の数値フォーマットを割り当てることができます。
NORMSDST 関数の使用
NORMSDST 関数は、Z 値を計算し、百分位数を取得します。
DEFINE FILE GGPRODS -* CONVERT SIZE FIELD TO DOUBLE PRECISION X/D12.5 = SIZE; END TABLE FILE GGPRODS SUM X NOPRINT CNT.X NOPRINT -* CALCULATE MEAN AND STANDARD DEVIATION COMPUTE NUM/D12.5 = CNT.X; NOPRINT COMPUTE MEAN/D12.5 = AVE.X; NOPRINT COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT PRINT SIZE X NOPRINT -* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION COMPUTE Z/D12.5 = (X - MEAN)/STDEV; COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8'); BY PRODUCT_ID NOPRINT END
出力結果は次のとおりです。
Size Z NORMSD ---- - ------ 16 -.07298 .47091 12 -.80273 .21106 12 -.80273 .21106 20 .65678 .74434 24 1.38654 .91721 20 .65678 .74434 24 1.38654 .91721 16 -.07298 .47091 12 -.80273 .21106 8 -1.53249 .06270
NORMSINV - 逆累積標準正規分布を計算
NORMSINV 関数は、標準正規分布で計算を実行し、標準正規分布上での百分位数の上限を形成する正規化値を求めます。これは、NORMSDST の逆です。NORMSDST についての詳細は、NORMSDST および NORMSINV - 標準正規分布の計算を参照してください。
NORMSINV の結果は、6 桁の倍精度小数点数として返されます。
逆累積標準正規分布関数を計算
NORMSINV(value, 'D8');
説明
標準正規分布上の百分位数を表す 0 (ゼロ) と 1 の間の数値です。
結果のフォーマットです。関数により返される値のフォーマットは倍精度小数点数です。有効な任意の数値フォーマットを割り当てることができます。
NORMSINV 関数の使用
NORMSDST 関数は、Z フィールドの百分位数を求めます。次に NORMSINV 関数が、この百分位数を正規化値として返します。
DEFINE FILE GGPRODS -* CONVERT SIZE FIELD TO DOUBLE PRECISION X/D12.5 = SIZE; END TABLE FILE GGPRODS SUM X NOPRINT CNT.X NOPRINT -* CALCULATE MEAN AND STANDARD DEVIATION COMPUTE NUM/D12.5 = CNT.X; NOPRINT COMPUTE MEAN/D12.5 = AVE.X; NOPRINT COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT PRINT SIZE X NOPRINT -* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION -* THEN USE RETURNED VALUES AS INPUT TO NORMSINV FUNCTION -* AND CONVERT BACK TO DATA VALUES COMPUTE Z/D12.5 = (X - MEAN)/STDEV; COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8'); COMPUTE NORMSI/D12.5 = NORMSINV(NORMSD, 'D8'); COMPUTE DSIZE/D12 = NORMSI * STDEV + MEAN; BY PRODUCT_ID NOPRINT END
出力では、NORMSINV 関数が NORMSDST 関数と逆方向の計算を実行した結果、元の値が返されています。
Size Z NORMSD NORMSI DSIZE ---- - ------ ------ ----- 16 -.07298 .47091 -.07298 16 12 -.80273 .21106 -.80273 12 12 -.80273 .21106 -.80273 12 20 .65678 .74434 .65678 20 24 1.38654 .91721 1.38654 24 20 .65678 .74434 .65678 20 24 1.38654 .91721 1.38654 24 16 -.07298 .47091 -.07298 16 12 -.80273 .21106 -.80273 12 8 -1.53249 .06270 -1.53249 8