OUTLIER: Identifying Outliers in Numeric Data
The 1.5 * IQR (Inner Quartile Range) rule is a common way to identify outliers in data. This rule defines an outlier as a value that is above or below 1.5 times the inner quartile range in the data. The inner quartile range is based on sorting the data values, dividing it into equal quarters, and calculating the range of values between the first quartile (the value one quarter of the way through the sorted data) and third quartile (the value three quarters of the way through the sorted data). The value that is 1.5 times below the inner quartile range is called the lower fence, and the value that is 1.5 times above the inner quartile range is called the upper fence.
OUTLIER is not supported in a DEFINE expression. It can be used in a COMPUTE expression or a WHERE, WHERE TOTAL, or WHERE_GROUPED phrase.
Given a numeric field as input, OUTLIER returns one of the following values for each value of the field, using the 1.5 * IQR rule:
- 0 (zero). The value is not an outlier.
- -1. The value is below the lower fence.
- 1. The value is above the upper fence.
Identify Outliers in Numeric Data
OUTLIER(input_field)
where:
Numeric
Is the numeric field to be analyzed.
Identifying Outliers
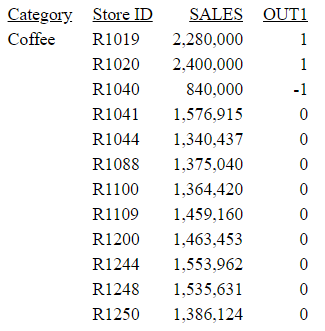
The following request defines the SALES field to have different values depending on the store code, and uses OUTLIER to determine whether each field value is an outlier.
DEFINE FILE GGSALES SALES/D12 = IF ((CATEGORY EQ 'Coffee') AND (STCD EQ 'R1019')) THEN 19000 ELSE IF ((CATEGORY EQ 'Coffee') AND (STCD EQ 'R1020')) THEN 20000 ELSE IF ((CATEGORY EQ 'Coffee') AND (STCD EQ 'R1040')) THEN 7000 ELSE DOLLARS; END TABLE FILE GGSALES SUM SALES COMPUTE OUT1/I3 = OUTLIER(SALES); BY CATEGORY BY STCD WHERE CATEGORY EQ 'Coffee' ON TABLE SET PAGE NOLEAD ON TABLE SET STYLE * GRID=OFF,$ ENDSTYLE END
The output is shown in the following image. Values above 2 million are above the upper fence, values below 1 million are below the lower fence, and other values are not outliers: