데이터 상관성 분석 이론
데이터 상관성 분석 도구는 어떤 컬럼 조합에 대한 확률 값(p값)을 계산합니다. 이 p값은 컬럼 간 연결이 통계적으로 의미가 있는지 여부를 결정하는 데 사용할 수 있습니다.
- 선형 회귀(숫자 대 숫자)
- 스피어만 상관계수(R)(숫자 대 숫자)
- 변량 분석(숫자 대 범주)
- 크러스컬-월리스(숫자 대 범주)
- 카이제곱(범주 대 범주)
선형 회귀
선형 회귀에 대한 수학적 설명은 데이터 상관성 분석 선형 회귀 알고리즘을 참조하십시오.
선형 회귀 옵션은 독립 변수 X가 종속 변수 Y의 변형 중 의미 있는 비율을 예측하는지 여부를 검증하는 F 테스트를 계산하는 데 사용됩니다.
선형 회귀 또는 "최소 제곱" 방법은 회귀 라인에서 점의 수직 거리의 제곱 합계를 최소화하여 상관계수를 얻습니다. 상관계수는 -1에서 +1 사이의 값을 가질 수 있습니다. 완벽한 음의 상관 관계가 있는 경우 R=-1이 되며, 완벽한 양의 상관 관계가 있으면 R=+1이 됩니다. R=0이면 상관 관계가 전혀 없고 두 컬럼은 서로 완전히 독립적인 관계입니다.
스피어만 상관계수(R)
스피어만 상관계수(R)에 대한 수학적 설명은 데이터 상관성 분석 스피어만 상관계수(R) 알고리즘을 참조하십시오.
스피어만 상관계수(R) 옵션은 상관계수의 비 매개변수적 계수를 계산하는 데 사용됩니다. 이것은 변수들의 순위를 매길 수 있는 경우에 사용합니다. 이것은 계산에 사용되는 값의 순위일 뿐이므로 기본적인 분포군을 알 수 없는 경우에도 각 행에 순위를 할당할 수만 있다면 사용 가능합니다. 선형 회귀와 마찬가지로 상관계수도 -1에서 +1 사이의 값을 가질 수 있습니다.
변량 분석
변량 분석에 대한 수학적 설명은 데이터 상관성 변량 분석 알고리즘을 참조하십시오.
Anova는 변량 분석을 의미합니다. 변량 분석 옵션은 범주 컬럼이 값 컬럼을 어떻게 범주화하는지를 검증하는 데 사용합니다. 범주 컬럼 및 값 컬럼의 조합에 대해 이 도구로 범주 컬럼이 값 컬럼의 값을 예측하는 정도를 나타내는 p값을 계산합니다. 낮은 p값은 두 컬럼 간의 강력한 연결 가능성을 나타냅니다.
8개 대상에 관한 데이터를 나타내는 다음 산점도를 예로 듭니다. 성별(남성/여성), 자가용 소유(있음/없음), 소득(달러), 키(cm). 소득은 수평 축에, 키는 수직 축에 분포합니다.
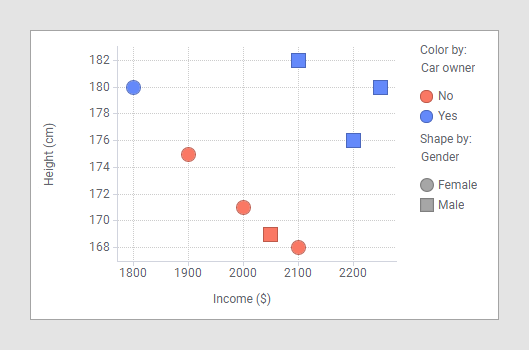
파란색 마커는 자가용 소유자, 빨간색 마커는 자가용 비 소유자를 나타냅니다. 사각형은 남성, 원은 여성을 나타냅니다. 성별 및 자가용을 범주 컬럼으로, 소득과 키를 값 컬럼으로 사용하여 변량 분석 계산을 수행하면 다음과 같은 4개 p값이 산출됩니다.
| 값 컬럼 | 범주 컬럼 | p값 |
|---|---|---|
| 키 | 자가용 | 0.00464 |
| 소득 | 성별 | 0.0447 |
| 키 | 성별 | 0.433 |
| 소득 | 자가용 | 0.519 |
낮은 p값은 범주 및 값 컬럼 사이에 연관성이 있을 가능성이 더 높음을 의미합니다. 이 경우에는 키와 자가용이 매우 관계 있어 보이고 소득과 자가용은 그렇지 않아 보입니다. 산점도를 조사하여 이를 검증할 수 있습니다.
이 도구와 함께 사용할 수 있는 데이터에 대한 자세한 내용은 데이터 상관성 분석에 대한 입력 데이터 요구 사항을 참조하십시오.
크러스컬-월리스
크러스컬-월리스 테스트에 대한 수학적 설명은 데이터 상관성 분석 크러스컬-월리스 알고리즘을 참조하십시오.
크러스컬-월리스 옵션은 독립된 샘플 데이터 그룹을 비교하는 데 사용합니다. 이것은 일방향 변량 분석의 비 매개변수적 버전이며 독립된 두 샘플에 대한 윌콕슨 테스트의 일반화입니다. 이 테스트에서는 실제 값 대신 데이터 순위를 사용하여 테스트 통계를 계산합니다. 정상 또는 균등한 분포가 충족되지 않을 경우 이 테스트를 변량 분석 대신 사용할 수 있습니다.
카이제곱
카이제곱 계산에 대한 수학적 설명은 데이터 상관성 분석 카이제곱 독립 테스트 알고리즘을 참조하십시오.
카이제곱 옵션은 관찰된 데이터를 특정한 가설(예를 들어, 예상 결과 및 관찰 결과 사이에 의미 있는 차이가 없다는 null 가설)에 따라 예상되는 데이터와 비교하는 데 사용합니다. 카이제곱은 관찰 데이터와 예상 데이터의 차이를 제곱한 합계를 가능한 모든 범주에서 예상되는 데이터로 나눈 값입니다. 카이제곱 통계가 높은 것은 관찰 결과와 예상 결과의 차이가 크다는 것을 의미합니다.
카이제곱 통계를 이용하여 p값을 계산할 수 있습니다. 카이제곱 통계가 높으면 p값은 낮습니다. 일반적으로 확률이 0.05 이하이면 의미 있는 차이인 것으로 간주됩니다.
- 데이터 상관성 분석 선형 회귀 알고리즘
선형 회귀 옵션은 데이터 테이블에 비어 있는 값이 없다는 전제 하에 p값을 계산합니다. - 데이터 상관성 분석 스피어만 상관계수(R) 알고리즘
스피어만 상관계수(R) 옵션은 데이터 테이블에 비어 있는 값이 없다는 전제 하에 p값을 계산합니다. - 데이터 상관성 분석 변량 분석 알고리즘
변량 분석 옵션은 각 그룹의 데이터 평균 값을 비교하여 그룹 간 차이를 계산합니다. 결과는 그룹 평균 간에 차이가 없는 null 가설을 테스트하여 산출합니다. 보다 공식적으로 말하면 p값은 null 가설에서 실제 결과 또는 더 극단적인 결과의 확률입니다. - 데이터 상관성 분석 크러스컬-월리스 알고리즘
크러스컬-월리스 옵션은 데이터 테이블에 비어 있는 값이 없다는 전제 하에 p값을 계산합니다. - 데이터 상관성 분석 카이제곱 독립 테스트 알고리즘
카이제곱 옵션은 데이터 테이블에 비어 있는 값이 없다는 전제 하에 p값을 계산합니다. - 데이터 상관성 분석에 대한 입력 데이터 요구 사항
데이터 관계 도구는 데이터의 컬럼 쌍을 비교하는 데 사용됩니다. 좋은 결과를 얻기 위해서 입력 데이터에 대한 특정 요구 사항이 있습니다.