Relations de données - Algorithme de l'Anova

L'option Anova calcule les différences entre les groupes en comparant les moyennes des données pour chaque groupe. Les résultats sont obtenus en testant l'hypothèse nulle, selon laquelle toutes les moyennes des différents groupes sont égales. Plus exactement, dans l'hypothèse nulle la variable p représente la probabilité du résultat actuel ou plus extrême.

Remarque : Si des valeurs manquent dans une table de données, cette table sera d'abord réduite à des lignes comprenant à la fois des valeurs de la première et de la deuxième colonnes.

Pour chaque ensemble de colonnes de catégories et de valeurs, la variable p est calculée comme suit :

Les lignes sont regroupées en fonction de leur valeur dans la colonne de catégorie.
La moyenne totale de la colonne de valeurs est calculée.
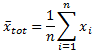
La moyenne de chaque groupe est calculée.
Les différences entre la variable et la moyenne pour un groupe sont calculées et élevées au carré.
Les carrés des différences sont ajoutés. Le résultat obtenu est une valeur associée à l'écart total des lignes par rapport à la moyenne de leurs groupes respectifs. Cette valeur est la somme des carrés intra groupes ou S2Wthn.
Pour chaque groupe, la différence entre la moyenne totale et la moyenne du groupe est élevée au carré et multipliée par le nombre de variables du groupe. Les résultats sont additionnés. Ce résultat désigne la somme des carrés inter groupes ou S2Btwn.
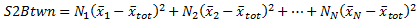
Les deux sommes des carrés permettent d'obtenir une statistique pour tester l'hypothèse nulle, appelée statistique F. Pour calculer une statistique F :

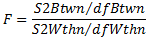
où dfBtwn (degré de liberté entre les groupes) est égal au nombre de groupes moins 1 et dfWthn (degré de liberté dans les groupes) est égal au nombre total de valeurs moins le nombre de groupes.
Une statistique F est répartie en fonction de la distribution F (généralement décrite dans les tableaux ou manuels mathématiques). La statistique F, associée aux degrés de liberté et à un tableau de la distribution F, détermine la variable p.

La variable p désigne la probabilité du résultat actuel ou plus extrême dans l'hypothèse nulle. Plus la variable p est basse, plus la différence est élevée.

Remarque : une très petite variable p peut également survenir si l'effet est minuscule alors que les tailles des échantillons sont importantes. De même, une variable p plus grande peut survenir si l'effet est important et la taille des échantillons est petite. Cela est dû au fait que l'hypothèse teste si l'effet est nul ou non.

Références

Arnold, Steven F., The Theory of Linear Models and Multivariate Analysis.