残差与拟合

残差与拟合图表是一种可在 Y 轴显示残差 X 轴显示拟合的散点图。您可以通过进行一次线性拟合来做比较，然后翻转拟合线使之变得水平。使用残差 0 的值是那些将直接在预计回归线上结束的值。残差与拟合图通常用于检测非线性度、不平等的误差方差和离群值。

形状（夸张）	结论
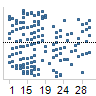
	如果线性回归模型适用于数据集，残差将或多或少地随机分布在 0 线周围。
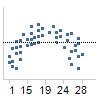
	如果残差在图表中形成一种模式，则当前模型可能不适合数据。

正态分位数

正态分位数图表可以计算列中所有值的正态分位数。值（Y 轴）将根据正态分位数（X 轴）进行标绘。

需要查看的内容：

形状（夸张）	结论
	近似正态分布。
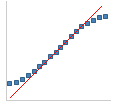
	方差比预期少。尽管此分布与正态分布不同，但是在统计计算中却很少带来问题。
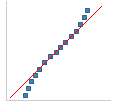
	比您在正态分布中预期的方差要多。
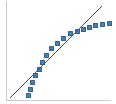
	分布中左偏。
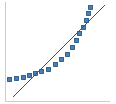
	分布中右偏。
	离群值。离群值会扰乱统计分析，因此应对其进行彻底调查。如果离群值是由于已知错误引起的，那么在执行更详细的分析之前应将其从数据中删除。

刻度 - 距离

刻度 – 距离图与残差与拟合图类似，不过是使用残差的平方根值而不是线性残差。其用于揭示残差幅度中的趋势。对于良好模型，其值应或多或少地随机分布。

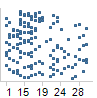
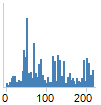
库克距离

库克距离是对尝试识别那些对预计系数具有更多影响的值的一种统计。条形图中的高峰可能表示应进一步调查的值，因为这些值对系数会产生较大影响。

效果与拟合或预测

效果与拟合或效果与预测图表是一种散点图，其中包含效果变量比对模型的拟合值，或效果变量比对从新数据使用先前计算的模型计算的预测值。此图的理想形状是所有点在一条线上，其中截距为 0，斜率为 1（大概 45 度角）。这将表明效果值和从模型计算的值完美匹配。事实上，这些点将位于 (0,1) 线周围的斜角范围。大大偏离此范围的点表示模型中的离群值或缺陷。

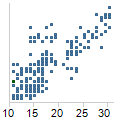
通常，残差与拟合或预测值散点图是诊断模型缺陷的一种较好图表，因为偏差集中围绕在水平线 (y=0) 而非 (0,1) 线周围。

预测概率柱形图

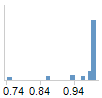
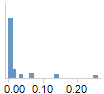
预测概率是一种有关效果变量的特定级别的预测概率的柱形图。对于两级别效果，您希望一个柱形图中的所有值接近一，而另一个柱形图中的所有值则应接近零。

ROC 曲线

ROC 或受试者操作特征曲线能够在类预测的阈值变化时显示分类器的性能。它是一种分类器的灵敏度（或叫真阳性率）比对 1- 特异度（或叫假阳性率）的图。真阳性率是真阳性中预测为阳性的数量；真阴性率是假阳性中预测为阴性的数量。预测的阳性和阴性随类预测值阈值的变化而变化。

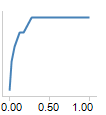
例如，在类 A 和 B 中，如果类 A 的阈值设置为很低（接近零），那么所有树类 A 观测值都将分类为 A（灵敏度为一）。但是，由于较大的假阳性率缘故，很多类 B 观测值也将错误地分类为 A。理想的 ROC 曲线开始于 (0.0)，上升至 (0,1)，然后转至 (1,1)。

随机分配预测类将产生一条 ROC 曲线，是一条从 (0,0) 到 (1,1) 斜率为 1 的曲线。

变量重要性图块

变量重要性图块显示各个预测器在模型中的重要性。对于参数模型（线性回归和逻辑回归），重要性值是模型中术语的检验统计量的绝对值。检验统计量越大，术语越重要。对于树型模型（回归和分类），变量重要性是在其中使用变量的各个拆分的拆分度量拟合度之和。这些值以百分比为刻度 - 百分比越大，变量在模型中越重要。