曲线拟合理论
通常，曲线拟合算法通过最小化选定的绩效函数来确定最佳拟合参数。为优化绩效函数，必须选择一组初始参数估计值，然后迭代优化绩效参数，直至绩效参数在迭代之间没有显著变化。在当前实施中，已将 Levenberg-Marquardt 算法用于非线性最小二乘法。
拟合度显示为 R2 值。R2 = 1.0 表示完美拟合，而 R2 = 0.0 表示回归模型可能不适用于该数据类型。
R2
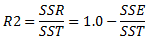
其中
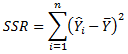（回归平方和）
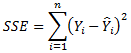（残差或误差平方和）
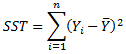（总平方和，SST= SSE+SSR）
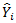表示因变量 Y 的第 i 个拟合值（使用选定模型计算得出）。
曲线拟合的限制
由于曲线计算是一个迭代过程，因此计算必须在某处停止。在某些情况下，在计算出最佳曲线之前，可能会达到最大迭代数。在该情况下，在图表的标题栏中会显示消息来告知您此情况。在某些情况下，例如，如果数据分布得特别分散或可用的数据点过少，那么迭代过程还可能生成收敛于错误最小值的曲线。
当在数据分析期间应用模型时，不仅查看 R2 值和曲线与曲线散点图中的当前标记的拟合程度十分重要，而且考虑对于更多极值，曲线的外观并确定模型在科学或统计上下文中是否合理也十分重要。为获得唯一曲线，唯一 x 值的数量必须大于或等于自由度的数目。如果可以通过无限多的方法解决曲线，则不能肯定显示的曲线与您的数据相关。
一般参考
Heath, M.T., (2002), Scientific Computing:An Introductory Survey, 2nd ed., McGraw-Hill, New York.
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A., Sorensen, D., (1999), LAPACK Users' Guide, 3rd ed., Society for Industrial and Applied Mathematics, Philadelphia, PA, ISBN = 0-89871-447-8
Holt-Winters Forecast 参考
Rob J Hyndman and George Athanasopoulos (2013), Forecasting:principles and practice. http://otests.com/fpp/7/1.
Rob J. Hyndman, Anne B Koehler, J. Keith Ord, and Ralph D. Snyder (2008), Forecasting with Exponential Smoothing: the state space approach, Springer.