Wide Data Variable Selector - Chi Square/Anova
This operator produces a new data set with chi-square or anova results with the significance statistics for each predictor (X) variable against a user-specified dependent (Y) variable from a very large data set, that is, the number of variables could be large - thousands or millions.
![]()
Information at a Glance
|
Parameter |
Description |
|---|---|
| Category | Transform |
| Data source type | TIBCO® Data Virtualization |
| Send output to other operators | Yes |
| Data processing tool | TIBCO® DV, Apache Spark 3.2 or later |
Algorithm
For each predictor (X) variable, the operator computes the correlation against the dependent (Y) variable. For each predictor (X) variable, the operator computes the chi-square or one-way analysis of variance (ANOVA) results against the dependent (Y) variable. For the categorical dependent variables, you can calculate the chi-square analysis, and for the continuous dependent variables, you can calculate the analysis of variance (ANOVA). Here, all the predictors are treated as categorical. If continuous predictors exist, they are converted to categorical predictors using a binning procedure before the results are calculated. The algorithm makes two passes through the data, one to collect the dependent values and another to calculate the correlations.
The scalability should not be limited by anything other than available cluster resources.
Input
An input is a single tabular data set that contains key-value pairs of variables and values in a stacked format, with the variable names (vars), continuous value (con_vals), categorical values (cat_vals), and the row id (id) columns. If the variable is continuous, then the values of the variable cat_vals should be null, and if the variable is categorical, then the values of the variable cont_vals should be null.
One of the continuous values and categorical values variables always have missing values - this is as expected based on the structure logic of an input data. If both of them are empty, the point is not used in the analysis calculations for the variable in question. In other words, statistics are calculated from all available and not the missing pairs of values separately for each predictor, not dependent on missing values in other predictors.
The operation checks for the validity of the dependent variable specification. See the Algorithm section for more information.
- If the dependent variable is categorical, then it should be in a categorical values column and have discrete values (string, long, int).
- If you have continuous predictors as well as continuous dependent variables, then use the Wide Data Variable Selector - Correlations operator.
Configuration
| Parameter | Description |
|---|---|
| Notes | Notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk appears on the operator. |
| Dependent Variable Name | Specify the name of the dependent variable against which the chi-square is computed or the dependent continuous variable against which anova analysis is computed. If the dependent variable and predictors are continuous, then use the Wide Data Variable Selector - Correlations operator. |
| Variables Column | Specify the name of the column where the variable names are carried. It should contain the name of the dependent variable and predictors. |
| Continuous Values Column |
Specify the column that contains values for continuous variables. |
| Categorical Values Column |
Specify the column that contains values for categorical variables. |
| Row ID Column | Specify the name of the column that contains the row ID numbers. |
| Number Of Bins |
Specify the number of bins used for the discretization of continuous predictors. The bin boundaries are equidistant. Default: 10 |
| Chi Square Output | Specify the output. If you have a continuous dependent variable, select Anova, if you have a categorical dependent variable, select Chi-Square or Chi-Square with p values. The following values are available:
Default: Chi-Square |
| Output Schema | Specify the schema for the output table or view. |
| Output Table | Specify the table path and name where the output of the results is generated. By default, this is a unique table name based on your user ID, workflow ID, and operator. |
| Store Results | When set to Yes, the operator saves the results. If set to No, the operator does not save the results. |
Output
A tabular preview of the output data set that includes the Output and Summary tabs.
-
Summary: The default summary that includes the parameters selected and their values.
-
Output: A single tabular data set containing requested output statistics and the related significance levels for each predictor.
A single tabular data set that contains requested output statistics and the related significance levels for each predictor.
Example 1
The following example shows the calculation of the chi-square test for each predictor variable against a user-specified dependent variable using the Wide Data Variable Selector - Chi Square/Anova operator.

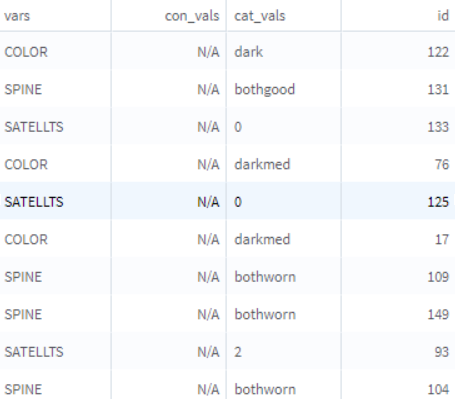
Data
A data set contains data in a stacked format where variable names are in the vars column, and values of these variables are in con_vals or cat_vals columns based on the type of variable. The dependent variable for this example is SATELLTS, which is a categorical variable.
Parameter Setting
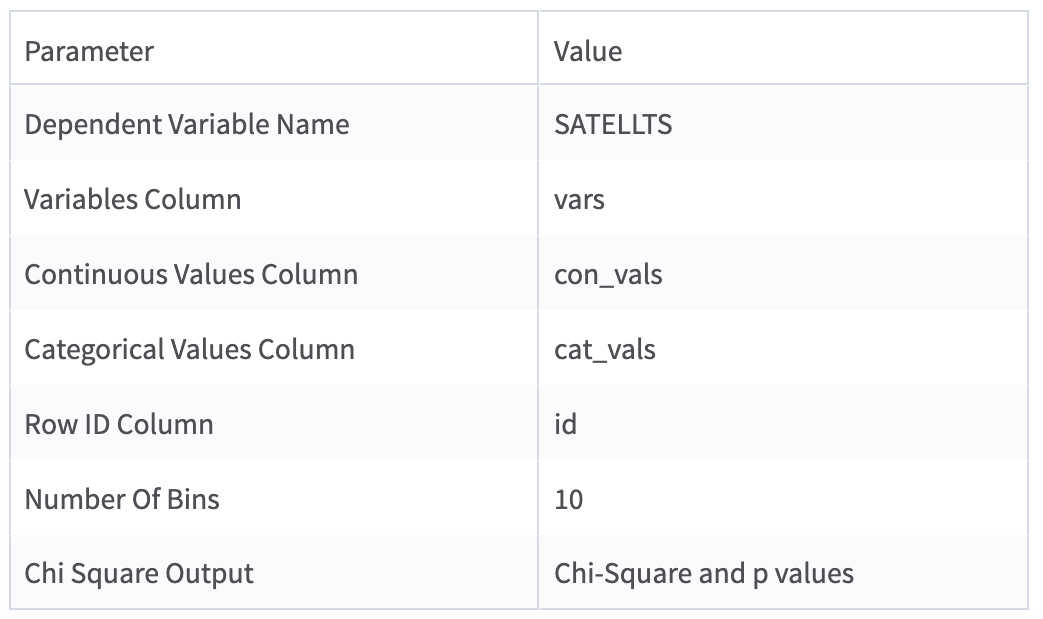
The parameter settings for this analysis are as follows:
-
Dependent Variable Name: SATELLTS
-
Variables Column: vars
-
Continuous Values Column: con_vals
-
Categorical Values Column: cat_vals
-
Row ID Column: id
-
Number Of Bins: 10
-
Chi Square Output: Chi-Square and p values
-
Store Results: Yes
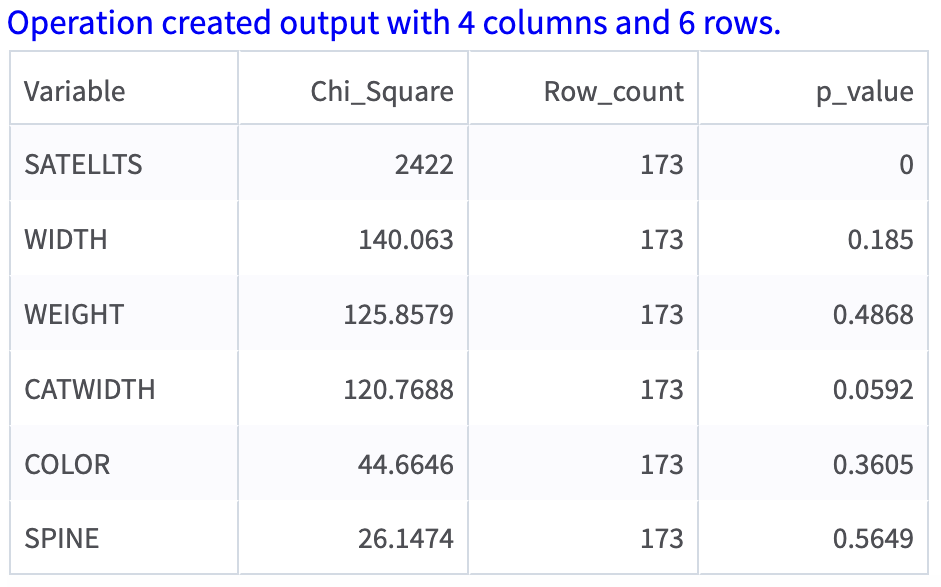
The following figures display the output results, one table with a summary of the parameters of analysis and the other with actual analysis results. The dependent variable SATELLTS is available in the output results, this represents the result where the SATELLTS versus SATELLTS test is conducted, and the p-value is 0, which means we are declining the hypothesis that both variables are independent.
Summary
Output
Example 2
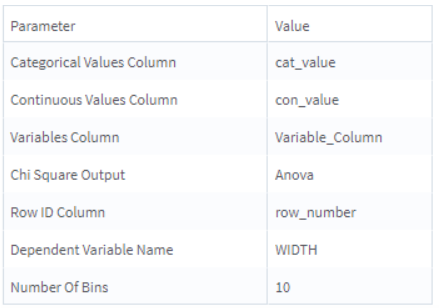
The following example shows the calculation of one-way ANOVA analysis separately for each predictor. The dependent variable is a user-specified continuous variable. The computation is done using the Wide Data Variable Selector - Chi Square/Anova operator.

Data
A data set contains data in a stacked format where variable names are in the vars column, and the values of these variables are in con_vals or cat_vals columns based on the type of variable. Here, the continuous dependent variable WIDTH.
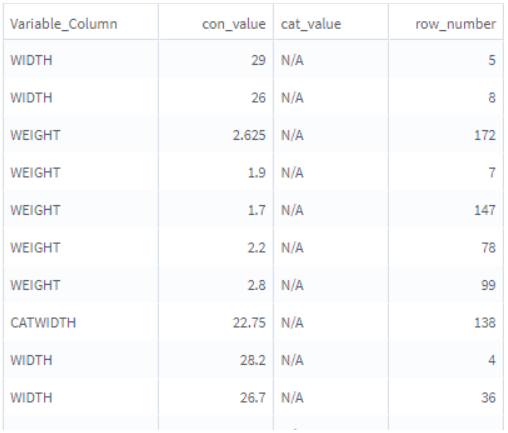
The following figures of the resulting output also show the parameter settings of the operator. The anova results are calculated where the dependent variable is WIDTH and the rest of the variables are predictors (continuous ones are converted for the purpose of this analysis into categorical variables with a defined number of bins).
Summary
Output
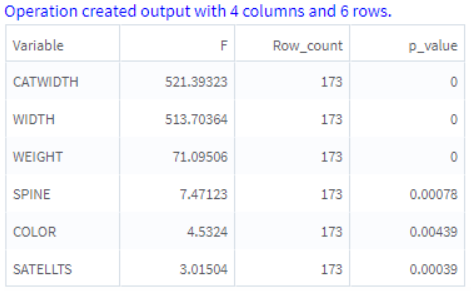
The large values of F statistic and significant p-value mean that the behavior of the dependent variable in groups of the predictor variable is significantly different. This means that there is a higher likelihood that the difference observed is real and not caused by chance.