Rows are grouped according to their value in the category column.
The total mean value of the value column is computed.
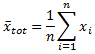
The mean within each group is computed.
The difference between each value and the mean value for the group is calculated and squared.
The squared difference values are added. The result is a value that relates to the total deviation of rows from the mean of their respective groups. This value is referred to as the sum of squares within groups, or S2Wthn.
For each group, the difference between the total mean and the group mean is squared and multiplied by the number of values in the group. The results are added. The result is referred to as the sum of squares between groups, or S2Btwn.
![]()
The two sums of squares are used to obtain a statistic for testing the null hypothesis, the so called F-statistic. The F-statistic is calculated as:
![]()
where dfBtwn (degree of freedom between groups) equals the number of groups minus 1, and dfWthn (degree of freedom within groups) equals the total number of values minus the number of groups.
The F-statistic is distributed according to the F-distribution (commonly presented in mathematical tables/handbooks). The F-statistic, in combination with the degrees of freedom and an F-distribution table, yields the p-value.