Data Relationships Chi-square Independence Test Algorithm

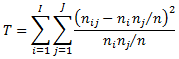
The Chi-square option calculates the p-value under the assumption that there are no empty values in the data table.

Note: If there are empty values in the data table, the data table will first be reduced to the rows containing values for both the first and the second column.

Let n be the total number of values and denote by I the number of unique values in the first column and by J the number of unique values in the second column. Also for i = 1, ..., I let n_i be the number of occurrences of the i^th unique value and for j = 1, ..., J, let n_j be the number of occurrences of the j^th unique value. If we now let n_ij denote the number of rows containing the i^th unique value in the first column and the j^th unique value in the second column, the Pearson's chi-square statistic is:

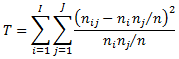
with (I-1)(J-1) degrees of freedom.

The p-value is then calculated from the chi-square distribution with (I-1)(J-1) degrees of freedom.

Reference:

Rice, John A., Mathematical Statistics and Data Analysis, 2nd ed., p 489-491.

Back to Overview of Data Relationships theory