Data Relationships Kruskal-Wallis Algorithm

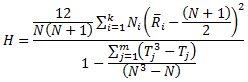
The Kruskal-Wallis option calculates the p-value under the assumption that there are no empty values in the data table.

Note: If there are empty values in the data table, the data table will first be reduced to the rows containing values for both the first and the second column.

The Kruskal-Wallis test can be seen as the nonparametric version of a one-way Anova. The test uses the ranks of the data rather than their actual values to calculate the test statistic. This test can be used as an alternative to the Anova, when the assumption of normality or equality of variance is not met.

For k groups of observations, all N observations are combined into one large sample, the result is sorted from smallest to largest values and ranks are assigned, assigning ties (when values occur more than once) the same rank.

Now, after regrouping the observations, the sum of the ranks are calculated in each group. The test statistic, H, is then:

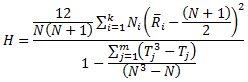
k = number of categories

N = number of cases in the sample

Ni = number of cases in the ith category

= average of the ranks in the ith category

Tj = ties for the jth unique rank

m = number of unique ranks

A p-value can be calculated from the test statistic by referring the value of H to a table with the chi-square distribution with k-1 degrees of freedom. This can be used to test the hypothesis that all k population distributions are identical.

Example:

For the following data table, the different parameters used in the test are as follows:

k = 2

N = 6

NA= 3

NB= 3

=2

=5

T1= 1

T2= 2

T3= 2

T4= 1

m = 4

H = 4.091

Reference:

Lehmann, E. L., Nonparametrics: Statistical Methods based on Ranks (1975), p. 204 – 210.

Back to Overview of Data Relationships theory