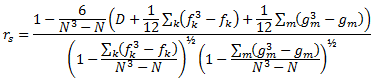
The Spearman R option calculates the p-value under the assumption that there are no empty values in the data table.
Note: If there are empty values in the data table, the data table will first be reduced to the rows containing values for both the first and the second column.
The Spearman R calculation is a nonparametric comparison based on the ranks of the observations, rather than on the values themselves. This test can be used as an alternative to the Linear Regression, when the assumption of normality or equality of variance is not met. For example, this is useful on occasions where outliers contribute too much to the calculations in a parametric test.
Spearman R can be calculated in several different ways depending on whether or not ties are common in the data table , that is, if several values are identical and thus have the same rank. Since it is quite common with ties in general data analysis, TIBCO Spotfire uses an algorithm where these can be handled. When ties occur, they are all given the mean of the ranks that they would have had if they had not been exactly identical (see Ranking Functions, "ties.method=average").
The correlation value is calculated according to:
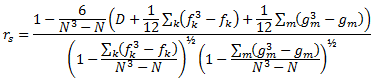
where
N = the number of valid pairs of measurements (xi, yi),
fk= the number of ties in the kth group of ties among the Y-column values
and
gm= the number of ties in the mth group of ties among the X-column values.
The test statistic, FStat is then:
![]()
where
rs2= RSq = the squared correlation value.
In TIBCO Spotfire, the Spearman t method has then been applied to calculate the p-values. This method has been chosen in order to allow the same calculation method to be used at all times and with an acceptable performance. The Spearman exact method is not suitable for cases with a lot of ties in the data. The Spearman Monte-Carlo method is suitable for any type of data, but when a lot of p-values are to be calculated then this method has too low performance.
References:
Lehmann, E. L., Nonparametrics: Statistical Methods based on Ranks (1975), p. 297 – 303.
Kendall, M., Rank Correlation Methods (1948), p. 37-54.
Back to Overview of Data Relationships theory