Advanced Example 5: Specifying a Process-Mixture Design

An example of a very complex type of design that can be analyzed using the general linear model is the process-mixture design, that is, a mixture design that also includes additional variables called process variables (for standard mixture designs, see also Mixture surface regression or the discussion of Mixture designs and triangular surfaces in Experimental Design). Cornell (1990b) defines process variables as factors in an experiment that do not form any portion of the mixture but whose levels, when varied, could affect the blending properties of the ingredients.

The process-mixture design includes the effects in the full factorial design for all the variables minus the effects in the full factorial design of the process variables. In most general linear model programs, such designs can be very difficult to specify; the non-standard factorial structure of the design requires that each effect in the design must be individually specified. Either a list of effects in the full-factorial design for all variables must be created and the appropriate effects deleted, or a list of only the appropriate effects to be included in the design must be created. Either way, correctly specifying the design is a tedious and error-prone task when there are more than just three or four variables.

STATISTICA GLM, however, provides two easy methods for specifying process-mixture designs. In the Analysis Wizard, a list of the effects in the full-factorial design for all variables can be generated. To this list, you can then append a list of the effects in the full-factorial design for the process variables. In the syntax editor, separating the two lists with a minus sign, that is, the deletion operator, produces the desired design. Equivalently, the full-factorial design for all variables can be compactly specified using the bar ( | ) operator, followed by the deletion ( - ) operator, followed by the full-factorial design for the process variables specified using the bar ( | ) operator (see the DESIGN keyword for a description of these syntax conventions). Using this second approach, each individual mixture variable is specified just once, each individual process variable is specified just twice, and one operator is specified between each variable name. This compares with the hundreds of variable names and operators required to specify the appropriate individual effects in process-mixture designs with five or more variables.

The example data file Procmix.sta presented by Cornell (1990b, p. 360) can be used to illustrate the specification of a process-mixture design in STATISTICA GLM. Mullet, Sheepshd, and Croaker are the mixture variables, Temp, Time, and Fry are the process variables, and Texture is the dependent variable.

Ribbon bar. Select the Home tab. In the File group, click the Open arrow and select Open Examples to display the Open a STATISTICA Data File dialog box. The Procmix.sta data file is located in the Datasets folder. Then, select the Statistics tab. In the Advanced/Multivariate group, click Advanced Models and from the menu, select General Linear to display the General Linear Models (GLM) Startup Panel.

Classic menus. On the File menu, select Open Examples to display the Open a STATISTICA Data File dialog box. The Procmix.sta data file is located in the Datasets folder. Next, from the Statistics - Advanced Linear/Nonlinear Models submenu, select General Linear Models to display the General Linear Models (GLM) Startup Panel.

Select General linear models as the Type of analysis and Analysis syntax editor as the Specification Method. Click the OK button to display the GLM Analysis Syntax Editor. Enter the following syntax into the Analysis syntax field:

Click the OK (Run) button to display the GLM Results dialog box.

Results

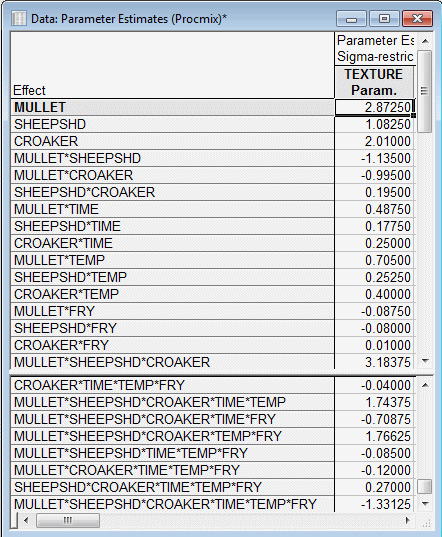
On the Summary tab, click the Coefficients button. The (abbreviated) spreadsheet below shows the effects that are generated and the respective parameter estimates.

Note that, as desired, there are no effects for the process variables except for their interactions with the mixture variables.

See also, GLM - Index.