Example 2: A 2 x 3 Between-Groups ANOVA Design
- Data File
- This example, based on a fictitious data set reported in Lindman (1974), begins with a simple analysis of a 2 x 3 complete factorial between-groups design.
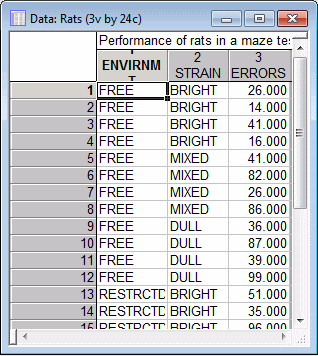
Suppose that we have conducted an experiment to address the nature vs. nurture question; specifically, we test the performance of different rats in the "T-maze." The T-maze is a simple maze, and the rats' task is to learn to run straight to the food placed in a particular location, without errors. Three strains of rats whose general ability to solve the T-maze can be described as bright, mixed, and dull, were used. From each of these strains, we rear 4 animals in a free (stimulating) environment, and 4 animals in a restricted environment. The dependent measure is the number of errors made by each rat while running the T-maze problem.
The data for this study are contained in the STATISTICA example data file Rats.sta. Open this data file:Ribbon bar. Select the Home tab. In the File group, click the Open arrow and from the menu, select Open Examples. The Open a STATISTICA Data File dialog box is displayed. Rats.sta is located in the Datasets folder.
Classic menus. From the File menu, select Open Examples to display the Open a STATISTICA Data File dialog box; Rats.sta is located in the Datasets folder.
A portion of this file is shown below.
- Specifying the Analysis
- Start the ANOVA analysis:
- Ribbon bar
- Select the Statistics tab, and in the Base group, click ANOVA.
- Classic menus
- Select ANOVA from the Statistics menu.
The General ANOVA/MANOVA Startup Panel will be displayed, in which we can enter the specifications for the design.
- Independent and dependent variables
- The ANOVA/MANOVA module classifies variables as either independent or dependent (see Elementary Concepts). Independent variables are those under the experimenter's control. We may also refer to these variables as grouping variables, coding variables, or between-group factors. These variables contain the codes that were used to uniquely identify to which group in the experiment the respective case belongs.
In the data file Rats.sta, the codes 1-free and 2-restricted were used in the categorical predictor variable Envirnmt to denote whether the rat belongs to the group of rats that were raised in the free or restricted environment, respectively. The codes used for the second independent variables (Strain) are 1-bright, 2-mixed, and 3-dull. The dependent variable in an experiment is the one that depends on or is affected by the independent variables; in this study this would be the variable Errors, which contains the number of errors made by the rats running the maze.
- Specifying the design
- In the
General ANOVA/MANOVA Startup Panel, select Factorial ANOVA as the Type of analysis and Quick specs dialog as the Specification Method. Then click the OK button to display the
ANOVA/MANOVA Factorial ANOVA dialog box. This is a 2 (Environment) by 3 (Strain) between-groups experimental factorial design.
Click the Variables button to display a standard variable selection dialog box. Select Errors on the Dependent variable list and Envirnmt and Strain on the Categorical predictors (factors) list, and then click the OK button.
Next, specify the codes that were used to uniquely identify the groups; click the Factor codes button and either enter each of the codes for each variable or click the All button for each variable to enter all of the codes for that variable. Finally, click the OK button. The ANOVA/MANOVA Factorial ANOVA dialog box will now look as follows:
- Reviewing the Results
- Click the OK button to run the analysis and display the
ANOVA Results dialog box.
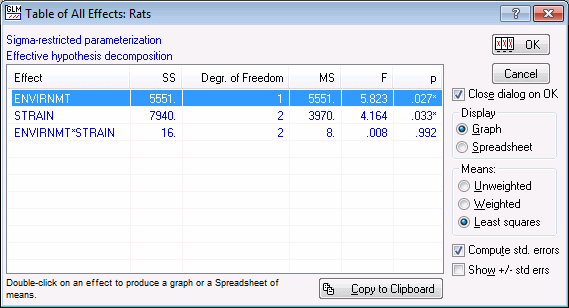
Click the All effects/Graphs button to display the table of all effects.
- Summary ANOVA table
- This table summarizes the main results of the analysis. Note that significant effects (p<.05) in this table are marked with an asterisk *. We can adjust the significance criterion (for highlighting) by entering the desired alpha level in the Significance level field on the Quick tab. Both of the main effects (Envirnmt and Strain) are statistically significant (p<.05) while the interaction is not (p>.05).
- Reviewing marginal means
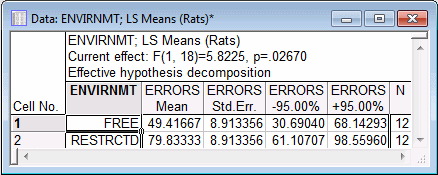
- The marginal means for the Envirnmt main effect will now be reviewed. (Note that the marginal means are calculated as least squares means.) Select the Envirnmt main effect select the Spreadsheet option button under Display; and then click the OK button to produce a spreadsheet with the table of marginal means for the selected effect.
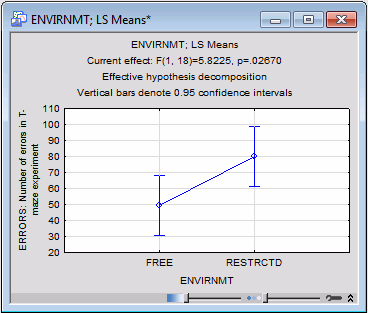
The default graph for all spreadsheets with marginal means is the means plot. In this case, the plot is rather simple. To produce this plot of the two means for the free and restricted environment, return to the Table of All Effects dialog box (by clicking the All effects/Graphs button on the Quick tab), change the Display option to Graph, and again click the OK button.
It appears that rats raised in the more restricted environment made more errors than rats raised in the free environment.
- Reviewing the interaction plot
- Now, let's look at all of the means simultaneously, that is, at the plot of the interaction of Envirnmt by Strain. Once again, return to the
Table of All Effects dialog box, and this time select the interaction effect (Environmt*Strain). Click the OK button, and the
Arrangement of Factors dialog box is displayed:
As you can see, we have full control over the order in which the factors in the interaction will be plotted. For this example, select STRAIN under x-axis, upper and ENVIRNMT under Line pattern (see above). Click the OK button, and the graph of means is displayed.
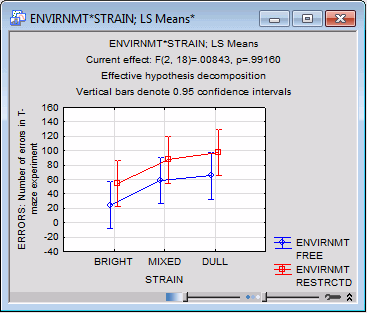
The graph, shown below, below nicely summarizes the results of this study, that is, the two main effects pattern. The rats raised in the restricted environment (dashed line) made more errors than those raised in the free environment (solid line). At the same time, the dull rats made the most errors, followed by the mixed rats, and the bright rats made the fewest number of errors.
- Post Hoc Comparisons of Means
- In the previous plot, we might ask whether the mixed strain of rats were significantly different from the dull and the bright strain. However, no a priori hypotheses about this question were specified, therefore, we should use post hoc comparisons to test the mean differences between strains of rats (refer to the Introductory Overview for an explanation of the logic of post hoc tests).
- Specifying post hoc tests
- After returning to the ANOVA Results dialog box, click the More results button to display the larger ANOVA Results dialog box, and then select the Post-hoc tab. For this example, select Strain in the Effect box in order to compare the (unweighted) marginal means for that effect.
- Choosing a test
- The different options for post hoc tests on this tab all "protect" us to some extent against capitalizing on chance (due to the post hoc nature of the comparisons, see ANOVA/MANOVA Introductory Overview - Contrast Analysis and Post-hoc Tests). All tests enable us to compare means under the assumption that we bring no a priori hypotheses to the study. These tests are discussed in the
Post-hoc tab topic. For now, select the Homogenous groups option button (in the Display group box) and click the Scheffé test button.
In this table, the means are sorted from smallest to largest, and the means that are not significantly different from each other have four "stars" (*) in the same column (i.e., they form a homogenous group of means); all means that do not share stars in the same column are significantly different from each other. Thus, and as discussed in Winer, Brown, and Michels (1991, p. 528), the only means that are significantly different from each other are the means group 1 (bright) and group 3 (dull). Thus, we would conclude that the dull strain of rats made significantly more errors than the bright strain of rats, while the mixed strain of rats is not significantly different from either.
- Testing Assumptions
- The ANOVA/MANOVA and GLM Introductory Overview - Assumptions and Effects of Violating Assumptions topic explains the assumptions underlying the use of ANOVA techniques. Now, we will review the data in terms of these assumptions. Return to the ANOVA Results dialog box and select the Assumptions tab, which contains options for many different tests and graphs; some are applicable only to more complex designs.
- Distribution of dependent variable
- ANOVA assumes that the distribution of the dependent variable (within groups) follows the normal distribution. We can view the distribution for all groups combined, or for only a selected group by selecting the group in the Effect drop-down box. For now, select the Environmt*Strain interaction effect, and click the Histograms button under Distribution of vars within groups. The
Select groups dialog box is first displayed, in which we can select to view the distribution for all groups combined or for only a selected group.
For this example, click the OK button to accept the default selection of All Groups, and a histogram of the distribution will be produced.
It appears as if the distribution across groups is multi-modal, that is to say, it has more than one "peak." We could have anticipated that, given the fact that strong main effects were found. If you want to test the homogeneity assumption more thoroughly, you could look at the distributions within individual groups.
For this example, a potentially more serious violation of the ANOVA assumptions will be tested.
- Correlation between mean and standard deviation
- As mentioned in the Introductory Overview, deviation from normality is not the major "enemy"; the most likely "trap" to fall into is to base our interpretations of an effect on an "extreme" cell in the design with much greater than average variability. Put another way, when the means and the standard deviations are correlated across cells of the design, the performance (alpha error rate) of the F-test deteriorates greatly, and we may reject the null hypothesis with p<.05 when the real p-value is possibly as high as .50!
Now, look at the correlation between the 6 means and standard deviations in this design. We can elect to plot the means vs. either the standard deviations or the variances by clicking the appropriate button (Plot means vs. std. deviations or Variances, respectively) on the Assumptions tab. For this example, click the Plot means vs. std. deviations button.
Note: in the illustration above, a linear fit and regression bands have been added to the plot via the Graph Options dialog box - Plot: Fitting tab and the Plot: Regr. Bands tab. Indeed, the means and standard deviations appear substantially correlated in this design. If an important decision were riding on this study, we would be well advised to double-check the significant main effects pattern by using for example, some nonparametric procedure (see the Nonparametrics module) that does not depend on raw scores (and variances) but rather on ranks. In any event, we should view these results with caution. - Homogeneity of variances
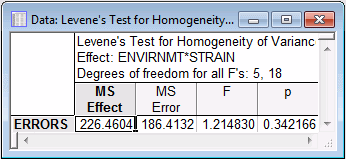
- Now, look at the homogeneity of variance tests. On the Assumptions tab, various tests are available in the Homogeneity of variances/covariances group. You may try a univariate test (Cochran C, Hartley, Bartlett) to compute the standard homogeneity of variances test, or the Levene's test, but neither will yield statistically significant results. Shown below is the Levene's Test for Homogeneity of Variances spreadsheet.
- Summary
- Besides illustrating the major functional aspects of the ANOVA/MANOVA module, this analysis has demonstrated how important it is to be able to graph data easily (e.g., to produce the scatterplot of means vs. standard deviations). Had we relied on nothing else but the F-tests of significance and the standard tests of homogeneity of variances, we would not have caught the potentially serious violation of assumptions that was detected in the scatterplot of means vs. standard deviations. As it stands, we would probably conclude that the effects of environment and genetic factors (Strain) both seem to have an (additive) effect on performance in the T-maze. However, the data should be further analyzed using nonparametric methods to ensure that the statistical significance (p) values from the ANOVA are not inflated.