数据关系 Kruskal-Wallis 算法
“Kruskal-Wallis”选项用于在假设数据表中不存在空值的前提下计算 p 值。
注： 如果数据表中存在空值，则首先要减少数据表行数，仅保留第一列和第二列均包含值的行。
可将 Kruskal-Wallis 检验视为非参数形式的单因素方差分析。这种检验方法使用数据等级（而非其实际值）来计算检验统计量。如果不满足正态或方差齐性假设，则可以使用这种检验方法替代方差分析。
对于 k 组观察值，将 N 个观察值全部合并为一个大容量样本，样本值按从小到大的顺序排列，并指定等级（为同一等级指定相同秩 [如果值出现多次]）。
对观察值重新分组之后，计算每组中的等级和。检验统计量 H 计算公式如下所示：
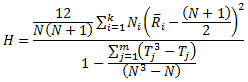
k = 类别数
N = 样本中的案例数
Ni = 第 i 个类别中的案例数
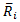= 第 i 个类别中等级的平均值
Tj = 第 j 个唯一等级的相同秩
m = 唯一等级数
使用 H 值查自由度为 k-1 的卡方分布表，从而根据检验统计量计算 p 值。这可用于检验 k 个总体分布全部相同的假设。
示例
对于以下数据表，检验中使用的不同参数如下所示：
| 数据表 | 参数 | ||
|---|---|---|---|
| 值列 | 值 | 等级 | 相同秩 |
| A | 1 | 1 | 1 |
| A | 3 | 2.5 | 2 |
| A | 3 | 2.5 | |
| B | 5 | 5.5 | 2 |
| B | 5 | 5.5 | |
| B | 4 | 4 | 1 |
k = 2
N = 6
NA= 3
NB= 3
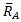=2
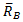=5
T1= 1
T2= 2
T3= 2
T4= 1
m = 4
H = 4.091
引用
Lehmann, E. L.，Nonparametrics:Statistical Methods based on Ranks (1975), p. 204-210.