数据关系理论

数据关系工具可以计算任何列组合的概率值（p 值）。此 p 值可用于确定列之间的相关性在统计上是否显著。

线性回归

有关线性回归的数学说明，请参见数据关系线性回归算法。

“线性回归”选项用于计算 F 检验统计量，调查自变量 X 是否可以预测因变量 Y 变动的很大一部分。

线性回归（即“最小二乘法”）通过最小化回归线上点的垂直距离的平方和获得相关系数。与线性回归相似，相关系数的值介于 -1 到 +1 之间。如果存在完全负相关，则 R = -1；如果存在完全正相关，则 R = +1。如果 R = 0，则表示完全不相关，这两列彼此完全独立。

注：与基本线性回归方法相比，使用截距和斜率运行线性回归会导致性能下降。出现这种情况的原因是一次完成的计算更多，以便可以在表中显示值，并且基本方法包括计算优化，其中 A 到 B 的比较结果与 B 到 A 的比较结果相同。使用截距和斜率变体无法实现这种优化，因此必须单独计算 B 到 A 组合。

有关斯皮尔曼等级的数学说明，请参见数据关系斯皮尔曼等级算法。

“斯皮尔曼等级”选项用于计算非参数形式的相关系数。用于可以对变量划分等级的情况。由于计算中仅涉及值的等级，因此即使基础分布族未知，只要可以为每一行指定等级，就可以使用斯皮尔曼等级。与线性回归相似，相关系数的值介于 -1 到 +1 之间。

有关方差分析的数学说明，请参见数据关系方差分析算法。

Anova 代表方差分析。“方差分析”选项用于调查类别列对值列进行分类的程度。对于每个类别列和值列组合，此工具可计算 p 值来表示类别列预测值列中值的程度。如果 p 值很小，表示两列之间可能显著相关。

假设以下散点图表示有关八个主体的数据：性别（男/女）、有车（是/否）、收入（美元）和身高（厘米）。横轴表示收入，纵轴表示身高。

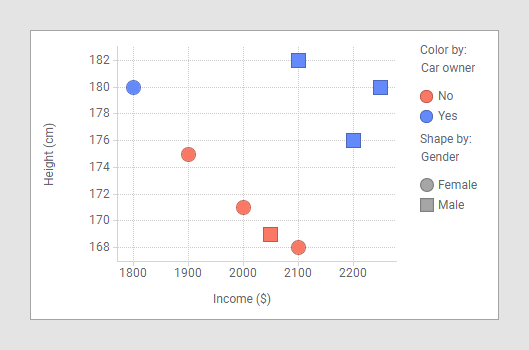
蓝色标记表示有车族，红色标记表示无车族。正方形表示男性，圆圈表示女性。如果将性别和汽车作为类别列、收入和身高作为值列执行方差分析计算，会得出以下四个 p 值：

如果 p 值很小，表示类别列和值列相关的概率较大。在本例中，身高和汽车不相关，而收入和汽车密切相关。可以通过查看散点图对此进行验证。

有关此工具所使用数据的详细信息，请参见为数据关系输入数据的要求。

有关 Kruskal-Wallis 检验的数学说明，请参见数据关系 Kruskal-Wallis 算法。

“Kruskal-Wallis”选项用于比较独立的抽样数据组。这种检验方法是非参数形式的单因素方差分析，并且是两个独立样本 Wilcoxon 检验的一般化。这种检验方法使用数据等级（而非其实际值）来计算检验统计量。如果不满足正态或方差齐性假设，则可以使用这种检验方法替代方差分析。

有关卡方计算的数学说明，请参见数据关系卡方独立性检验算法。

“卡方”选项用于比较观察数据与满足特定假设（例如无效假设，是指期望结果与观察结果之间不存在显著差异）的期望数据。卡方是观察数据与期望数据之间差值的平方和除以所有可能类别中的期望数据所得值。如果卡方统计量很大，表示观察数据与期望数据之间存在很大差异。

可以根据卡方统计量计算 p 值。如果卡方统计量很大，则此值很小。通常情况下，如果概率小于或等于 0.05，则认为存在显著差异。