PCA (DB)

Information at a Glance

Category	Model
Data source type	DB
Sends output to other operators	Yes
Data processing tool	n/a

Algorithm

PCA (Principal Component Analysis) is an orthogonal linear transformation that transforms data into a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, the third on the third coordinate, continuing until the number of rows has been reached or a preset maximum principal component threshold has been reached.

The Alpine PCA operator implements an eigenvalue decomposition of a data covariance matrix Σ (or, correlation matrix R).

Each principal component is a linear combination of the original variables.
The coefficients (loadings) are the eigenvectors (v1, v2,...vp) of covariance matrix Σ (or, correlation matrix R) with unit length.
The eigenvalues (λ1, λ2,...λp) denote the contribution of the principal component associated with it.
The principal components are sorted by descending order according to their variance contribution.
The user can choose the number of principal components according to the accumulation contribution (∑ij=1λj/∑pK=1λK).

More details are available in Principal Component Analysis, (1986), Joliffe, I.T.

Additional references:

Jerome Friedman, Trevor Hastie, Robert Tibshirani (2008), The Elements of Statistical Learning Data Mining, Inference and Prediction Chapter 3: "Linear Methods for Regression"
Joliffe, I.T. (1986), Principal Component Analysis, New York, Springer
Wu, W., Massart, D.L., and de Jong, S. (1997), "The Kernel PCA Algorithms for Wide Data. Part I: Theory and Algorithms" Chemometrics and Intelligent Laboratory Systems, 36, 165-172.

Input

A data set from the preceding operator.

Configuration

Parameter	Description
Notes	Schema where MADlib is installed in the database. MADlib must be installed in the same database as the input dataset. If a "madlib" schema exists in the database, this parameter defaults to madlib.
Analysis Type	The type of matrix to use to perform the eigenvalue decomposition. COV-POP (the default): Uncorrected covariance matrix. This implements the PCA algorithm against un-centered, un-scaled data. COV-SAM: Covariance matrix. This implements the PCA algorithm against centered but un-scaled data. CORR: Correlation matrix. This implements the PCA algorithm against centered and scaled data.
Percent	The threshold for the fraction of the variance explained with principal components. This decides the number of principal components. The value expected is between 0 and 1. A larger value directly relates to the number of principal components reported.
Result Output Schema	The schema name of the result output table transformed from the original table.
Result Output Table	The name of the result output table transformed from the original table.
Result Output Table Storage Parameters	For operators that can generate an output table, the Storage Parameters dialog box allows you to specify additional parameters regarding storage method and compression. See:Storage Parameters Dialog Box
Drop If Exists (Result)	If Yes (the default), drop the existing table of the same name and create a new one. If No, stop the flow and alert the user that an error has occurred.
Eigenvalues Output Schema	The schema name of the output table in which to save the scores of the principal components.
Eigenvalues Output Table	The name of the output table in which to save the scores of the principal components.
Eigenvalues Output Table Storage Parameters	The storage parameters of the output table in which to save the scores of the principal components.
Drop If Exists (Eigenvalues)	Specifies whether to overwrite the existing eigenvalues. Yes (the default) - If the entry with the name exists, it is dropped before storing the results. No - If the entry with the name exists, the results window displays an error message.
Column Names	Click Columns to open the dialog box for selecting the available columns from the procedure of PCA.
Carryover Columns	You can choose to keep columns from the input data untransformed and included in the output. To do this, click Carryover Columns to open the dialog box for selecting the columns to retain in the result table.

Output

Visual Output

Results Table

Provides the eigenvalues used in the matrix transformation.

Initial variable columns: The initial variable columns passed into the PCA operator are displayed, along with a magnitude value for that variable's contribution to the eigenvector transformation into each derived principal component.
alpine_pcadataindex: Eigenvector index number that provides a unique number for each derived principal component.
alpine_pcaevalue: Eigenvalue for that principal component.
alpine_pcacumvl: The fraction of the variability that this eigenvector explains for the principal component defined.
alpine_pcatotalcumvl: The cumulative fraction of the variability that this eigenvector explains for the principal component defined.

Output Table

Provides an overview of the new reduced Principal Components data set.

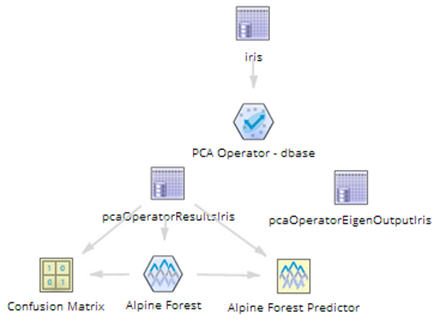
alpine_pcaattr[0-13]+: Each of the newly derived Principal Components columns is provided, along with their values for the new transformed data set. In this case, the source Iris data set with hundreds of variables was reduced to only 13 principal components variables and saved as pcaOperatorResultsIris. (See the example flow below.)

Carryover columns: any carryover columns from the original data set that were specified in the PCA operator configuration are displayed here, such as any necessary unique ID key or the dependent variable to predict in a following model. In this example, the "class" column was carried over to be used in a following Alpine Forest model.

Data Output

Stored database tables that can be accessed by other operators.

The PCA operator for the database is technically a terminal operator, meaning that no other operator directly follows it in the workflow. However, the PCA operator stores its Principal Component Results (and Eigenvalue Output details) in two database tables that can then be accessed as the data source for a new workflow, if applicable. The example below shows the results of the database PCA operator being saved as pcaOperatorResultsIris and pcaOperatoreEigenOutputIris. The tables can be brought into the workflow and the derived Principal Components can be fed into an Alpine Forest operator, for example, and the classification results analyzed in the Confusion Matrix in order to understand if the reduced set of variables that the PCA operator created provide an accurate enough model.

Contents

Index