Elastic Net Linear - MADlib
Team Studio supports the MADlib open-source implementation of the Elastic Net Linear Regression algorithm. This operator implements MADlib's open-source elastic net regularization algorithm for linear regression problems.
Algorithm
Elastic net regularization seeks to find a weight vector that, for any given training example set, minimizes a metric function that combines the L1 and L2 penalties of the lasso and ridge regression methods.
More information including general principles can be found in the official MADlib documentation.
Configuration
The following parameters must be set for minimal configuration.
| Parameter | Description |
|---|---|
| Notes | Any notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk is displayed on the operator. |
| MADlib Schema Name | The schema where MADlib is installed in the database. MADlib must be installed in the same database as the input data set. If a "madlib" schema exists in the database, this parameter defaults to madlib. |
| Model Output Schema Name | The name of the schema where the output is stored. |
| Model Output Table Name | The name of the table that is created to store the Regression model. The model output table stores the following.
family | features | features_selected | coef_nonzero | coef_all | intercept | log_likelihood | standardize | iteration_run See the official MADlib elastic net regularization documentation for more information. |
| Drop If Exists | |
| Dependent Variable | The quantity to model or predict. The list of the available data columns for the Elastic Net Linear operator are displayed. Select the data column to be considered the dependent variable for the regression. The dependent variable should be a numerical data type. |
| Independent Variables |
Allows the user to select the independent variable data columns to include for the regression analysis or model training. At least one column or one interaction variable must be specified.
Click Select Columns to open the Select Columns Dialog Box and select the available columns from the input data set for analysis. |
| Control Parameter | The elastic net control parameter (alpha) must be a value between 0 and 1, inclusive. |
| Regularization Parameter | Must be a positive value. |
| Standardize | Specifies whether to normalize the data. |
| Optimizer | Can be Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) or Incremental Gradient Descent (IGD). The required parameters for the optimizer configuration are dependent on the optimizer selected.
See the official MADlib elastic net regularization documentation for more information. |
| FISTA Maximum Stepsize | The initial backtracking step size. At each iteration, the algorithm first tries
stepsize = max_stepsize , and if it does not work, it then tries a smaller step size,
stepsize = stepsize/eta, where
eta must be larger than 1. At first, this seems to perform repeated iterations for even one step, but using a larger step size actually greatly increases the computation speed and minimizes the total number of iterations. A careful choice of
max_stepsize can decrease the computation time by more than 10 times.
Default value: 4.0. |
| FISTA Eta | If
stepsize does not work,
stepsize /eta is tried. Must be greater than 1.
Default value: 2.0. |
| Warmup | A value of
true specifies a series of lambda values, which is strictly descent and ends at the lambda value that the user wants to calculate, is used. The larger lambda gives a very sparse solution, and the sparse solution again is used as the initial guess for the next lambda's solution, which speeds up the computation for the next lambda. For larger data sets, this can sometimes accelerate the whole computation and may be faster than computation on only one lambda value.
A value of false (the default) specifies that this warmup procedure is not performed. |
| Warmup Lambdas | The lambda value series to use when Warmup is true. The default is NULL, which means that lambda values are automatically generated. |
| Number of Warmup Lambdas | The number of lambdas to use in
Warmup. If warmup_lambdas is not
NULL, this value is overridden by the number of provided lambda values.
Default value: 15. |
| Warmup Tolerance | The value of tolerance used during warmup.
Default value: 1e-6. |
| FISTA Use Active Method | A value of
true specifies an active-set method is used to speed up the computation. Considerable speedup is obtained by organizing the iterations around the active set of features - those with nonzero coefficients. After a complete cycle through all the variables, we iterate on only the active set until convergence. If another complete cycle does not change the active set, we are done; otherwise the process is repeated.
A value of false (the default) specifies that the active-set method is not used. |
| FISTA Active Tolerance | The value of tolerance used during active set calculation.
Default value: 1e-6. |
| FISTA Random Step Size | Whether to add some randomness to the step size. Sometimes, this can speed up the calculation.
Default value: 1e-6. |
| IGD Step Size | Initial backtracking step size.
Default value: 0.01. |
| IGD Zero Coefficient Threshold | When a coefficient is very small, set this coefficient to
0.
Due to the stochastic nature of SGD, only very small values can be obtained for the fitting coefficients. Therefore, threshold is needed at the end of the computation to screen out tiny values and hard-set them to zeros. This is accomplished as follows.
Default value: 1e-10. |
| IGD Parallelize | A value of
true specifies that the computation should be run on multiple segments.
SGD is a sequential algorithm in nature. When running in a distributed manner, each segment of the data runs its own SGD mode, and then the models are averaged to get a model for each iteration. This averaging might slow down the convergence speed, although the ability to process large data sets on multiple machines is also acquired. This algorithm, therefore, provides the parallel option to allow you to choose whether to do parallel computation. Default value: true. |
| Maximum Iterations | When the difference between coefficients of two consecutive iterations is smaller than the
Convergence Tolerance or the iteration number is larger than Maximum Iterations, the computation stops.
Default value: 10000. |
| Convergence Tolerance | When the difference between coefficients of two consecutive iterations is smaller than the Convergence Tolerance or the iteration number is larger than
Maximum Iterations, the computation stops.
Default value: 1e-6. |
| Draw Residual Plot | Specifies the option to draw the residual plot and Q-Q (Quantile-Quantile) plot used for model validation.
The residual plot displays a graph that shows the residuals of a linear regression model on the vertical axis and the independent variable on the horizontal axis. The Q-Q plot graphically compares the distribution of the residuals of a given variable to the normal distribution (represented by a straight line). Default value: true, meaning that the regression operator has two additional outputs showing the residual plot and Q-Q plot. |
Output
- Visual Output
- Results are displayed across the
Summary,
Residual Plot, and
Q-Q Plot tabs.
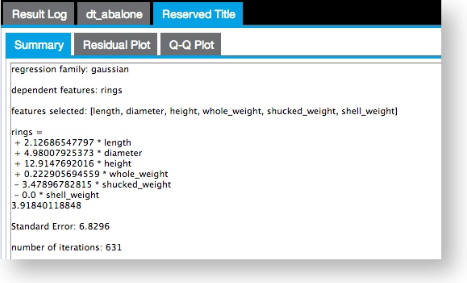
See the Linear Regression Operator documentation and Official MADlib elastic net regularization documentation for more information.
- Data Output
- None.

