Decision Tree

Information at a Glance

Category	Model
Data source type	HD
Sends output to other operators	No
Data processing tool	MapReduce

This topic applies to configuring a decision tree for Hadoop. To see information for database decision tree options, see Decision Tree - MADlib, Decision Tree Classification - CART, or Decision Tree Regression - CART. For more information about working with decision trees, see Classification Modeling with Decision Tree.

Algorithm

The Decision Tree operator implements a supervised classification algorithm. After the decision steps of the tree are learned, the Decision Tree algorithm is quick to evaluate the predicted classifications for new data.

The Decision Tree Operator implements a classification tree only, meaning its node labels represent a range of discrete values, as opposed to the CART Operator, which is both a classification and regression tree, with its labels representing a range of continuous (numeric) values.

Note: The Decision Tree Operator can split a node into more than just two sub-groups (that is, it is not restricted to being a binary tree like the CART Operator).

The Decision Tree Operator supports the C4.5 (Quinlan, 1993) deterministic method for constructing the decision tree structure, using information gain as the criteria. Therefore, the following is true.

At each node of the tree, C4.5 chooses one attribute of the data that most effectively splits its set of samples into subsets with one attribute value or another.
The attribute with the highest normalized information gain is chosen to make the decision and is placed higher in the tree compared to other attributes.
Information Gain measures the gain in purity from parent to children sub-nodes.
The C4.5 algorithm then recurses on the smaller sub-lists.
For pruning, the C4.5 algorithm employs a pessimistic pruning method that estimates error rates when making decisions regarding sub-tree pruning.

Input

A data set that contains the dependent and independent variables for modeling.

Configuration

For the Decision Tree Operator, the following relationship exists among the properties.

The tree-growth phase refers to the Minimal Gain and Maximal Depth configuration properties.
The pre-pruning phase refers to the Number of Pre-Pruning Alternatives, Minimal Leaf Size, and Minimal Size for Split configuration properties (in addition to the Minimal Gain and Maximal Depth parameters).
The pruning phase refers to the Confidence configuration property.

Parameter	Description
Notes	Any notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk is displayed on the operator.
Dependent Column	The quantity to model or predict. A Dependent Column must be specified for the decision tree. Select the data column to be considered the dependent variable for the regression. Dependent Column must be a categorical type (including integer), such as `eye color = blue, green, or brown`. Note: Null values are ignored during model training. If Dependent Column has three or more non-null values, a leaf node maps to each of the possible values.
Columns	Allows the user to select the independent variable data columns to include for the decision tree training. At least one column must be specified. Note: All data types are allowed for the column names. Each independent column is limited to 1,000 distinct values. The number of leaf nodes for each independent variable depends on the data (that is, there can be more than two leaf nodes in decision trees). Click Column Names to open the dialog box for selecting the available columns from the input data set for analysis.
Max Depth (-1=Unlimited)	Sets the "depth" of the tree or the maximum number of decision nodes it can branch out to beneath the root node. A tree stops growing any deeper if either a node becomes empty (that is, there are no more examples to split in the current node) or the depth of the tree exceeds this Maximal Depth limit. Maximal Depth is used during the tree-growth phase. The range of possible values is between -1 and any integer greater than 0. A value of -1 represents "no bound" - the tree can take on any size or number of decision nodes until the nodes become empty. Default value: 5.
Confidence	Specifies the confidence % boundary to use for the pessimistic error algorithm of pruning. Confidence controls the pruning phase of the decision tree algorithm. The pruning phase uses confidence intervals to estimate the "worst case" error rate of the node. The confidence level is the certainty factor or upper limit of the chance of an error being found in a leaf node. If the node has a error rate greater than this Confidence limit, it is pruned. It could be thought of as the probability of there being an incorrect classification in the leaf node. Setting a higher Confidence value allows the model to use nodes with higher individual error rates (less pruning). Setting a lower Confidence value is indicating less tolerance for error and, therefore, more pruning. Confidence applies only when pruning is set to true (that is, the No Pruning property is true). However it still must always be set to .50 or less or the system does not run - it would not make sense for there to be a greater than 50% chance of there being an error in a leaf node. Default value: 0.25, representing a 25% probability of there being an error in the leaf node classification set.
Minimal Gain	Specifies the threshold gain in purity from parent to child node that must be achieved between various decision node options in order to justify producing a split. Once a split results in less than the minimal information gain setting, that node is made a leaf node. Minimal Gain is used for the tree-growth phase. The range of possible values is any decimal value ≥ 0. The way this is phrased in information theory is as the threshold of the amount of entropy that must be removed by a node split based on a variable value. Default value: 0.1. This represents a limit of 10% information gain needing to be achieved in order to justify splitting the node.
Number of Pre-Pruning Alternatives	Specifies the maximum number of alternative nodes allowed when pre-pruning the tree. This property is only relevant when pre-pruning is set to true (that is, the No Pre-Pruning property is not checked). The independent variable columns are sorted by their score (that is, information gain) before splitting occurs. During the pre-pruning phase, if the column with the bigger score does not meet the minimal leaf size condition, the column is ignored for splitting, and the next column is checked until the column meeting the condition is found or the Number of Pre-Pruning Alternatives is met. The range of possible values is any integer ≥ 0. Default value: 3.
Min Size for Split	Specifies the minimal size (or number of members) of a node in the decision tree in order to allow a further split. If the node has fewer data members than the Minimal Size for Split, it must become a leaf or end node in the tree. The range of possible values is any integer ≥ 1. Minimal Size for Split is referenced during the pre-pruning phase. Default value: 4.
No Pruning	If true, no pruning is performed. If false (the default), pruning is performed.
No Pre-pruning	If true, no pre-pruning is performed. If false (the default), pre-pruning is performed. For more information, see Pruning or Pre-Pruning.
Min Leaf Size	Specifies the least number of data instances that can exist within a terminal leaf node of a decision tree. The range of possible values is any integer value ≥ 1. This setting limits the tree depth based on the size of the leaf nodes, ensuring enough data makes it to each part of the tree. This is useful, for example, when the model construction is taking too long or when the model shows very good ROC on training data but not nearly as good performance on hold-out or cross-validation data (due to over-fitting). For example, if the Minimal Leaf Size is 2, each terminal leaf node must contain at least 2 training data points. Default value: 2.
Category Limit	Limits the number of the categories into which a single categorical input column can split the data.
Numerical Granularity	Limits the number of the categories into which a single numerical input column can split the data.

Output

Visual Output

Highlight a decision tree node to see the decision criteria used to arrive at the node.

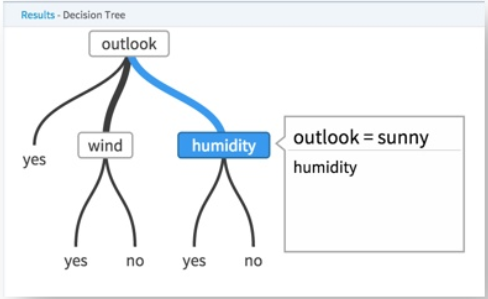
Decision trees need additional operators added to them in order to effectively analyze their effectiveness. Every decision tree modeling operator must be followed by a Predictor operator, which provides the prediction value for each data row compared against the actual data set training value and the associated confidence level.

The output from the Predictor operator looks like the following image.

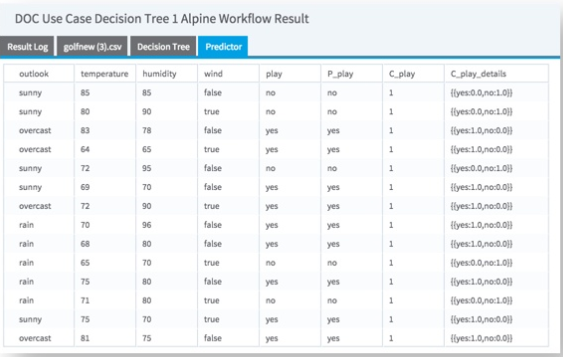
The P_play prediction column shows a value of yes or no and uses a threshold assumption of > than 50% confidence that the prediction will happen.

The C_play column indicates the confidence that the Dependent value will be 1.

Usually, C_play is a decimal value. In this example, the data set is small and created as an example.

The C_play details column indicates the confidence for each possible value of the dependent variable.

Using With Other Scoring Operators: Adding additional scoring operators, such as a ROC graph, is also helpful in immediately assessing how predictive the Decision Tree model is.

Data Output

None. This is a terminal operator.

Example

The following image shows a typical Analytic Flow configuration for Decision Tree operators.

Contents

Index