Naive Bayes (HD)
The Naive Bayes operator calculates the probability of a particular event occurring. It can be used to predict the probability of a certain data point being in a particular classification.
Information at a Glance
Algorithm
The Naive Bayes classifier calculates the probability of an event occurring. it combines Bayes' theorem with an assumption of strong independence among the predictors. Bayes' theorem calculates the probability of occurrence given a prior event has occurred. Regardless of actuality, a Naive Bayes classifier considers the influence of predictors on the outcome independently.
- The Team Studio Naive Bayes Operator computes the dependent variable's class priors and each of the independent variables' probability distributions using the Naive Bayes' conditional probability theorem, with the independence assumption.
- As an overview, the Naive Bayes conditional probability theorem says that, given a data set, X, and an outcome Hypothesis, H, the posterior probability that the Hypothesis is true is proportional to the product of the likelihood multiplied by the prior probability.
- Depending on the precise nature of the probability model, Naive Bayes classifiers can be trained very efficiently in a supervised learning setting.
- Given some data and some hypothesis, the posterior probability that the hypothesis is true is proportional to the product of the likelihood multiplied by the prior probability.
- For simplicity, the "prior probability" is often abbreviated as the "prior" and the "posterior probability" as the "posterior".
- The likelihood brings in the effect of the data, while the prior specifies the belief in the hypothesis before the data was observed.
More formally, the Bayes' formula for conditional probability is represented as
- P(H|X) is the conditional probability of outcome H happening given condition X
- P(X|H) is the conditional probability of the outcome X happening given condition H
- P(H) is the prior observed probability of the outcome H happening
- P(X) is the prior observed probability of the outcome X happening.
This Bayes formula is helpful because it provides a way to calculate the Posterior Probability, P(H|X), from P(H), P(X|H), and P(X), which can be calculated from historic data.
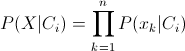 This is the Naive Bayes conditional independence assumption formula.
This is the Naive Bayes conditional independence assumption formula.
If the feature is a continuous value, the conditional distribution over the class variable C is expressed as follows:
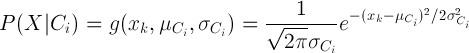
- This formula describes the ideal normal distribution curve for each independent variable's value. Note: This is a simplification assumption since most of the independent variables are likely to have exactly normal distributions.
- However, the Naive Bayes model predictions are still quite accurate with an acceptable level of confidence.
- The Naive Bayes Operator can accept a dependent column that has two or more discrete categories. Note: if the dependent variable is a numeric integer, each integer is treated as a separate category.
- The independence assumption treats all the predictors or variables as independently related to the outcome.
- The Naive Bayes theorem results give the normal probability curve of each possible categorical value occurring for that variable.
Configuration
In Naive Bayes configuration, Dependent Column is the value in the data set that is the predicted dependent variable, or "class" variable. Column(s) are the expected independent variable data columns, or parameters, to use for model training.
The Dependent Column must be a categorical (non-numeric) variable. Naive Bayes analysis predicts the odds of an outcome of a categorical variable based on one or more predictor variables. A categorical variable is one that can take on a limited number of values, levels, or categories, such as valid or invalid.
Unlike Logistic Regression and Decision Tree classifiers, Naive Bayes does not require a Value To Predict specification, because the output for the Naive Bayes operator provides the probability of the event for each observed classification value.
Output
- Visual Output
-
- Summary Results
- The
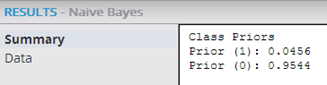
Summary results display the class priors, as follows.
Class Priors - The priors define the observed historical probability of the various possible classification outcome events for the dependent variable based on the training data for the model. This is helpful information because it shows an overall trend of the data for each possible outcome and allows a quick, intuitive check of the source data.
The modeler can see which of the possible dependent variable values occurred the most and least frequently in the training data.
In the example above, the training data showed a prior 4.56% occurrence of the Dependent Variable Class value being 1, and a 95.44% occurrence of the value being 0.
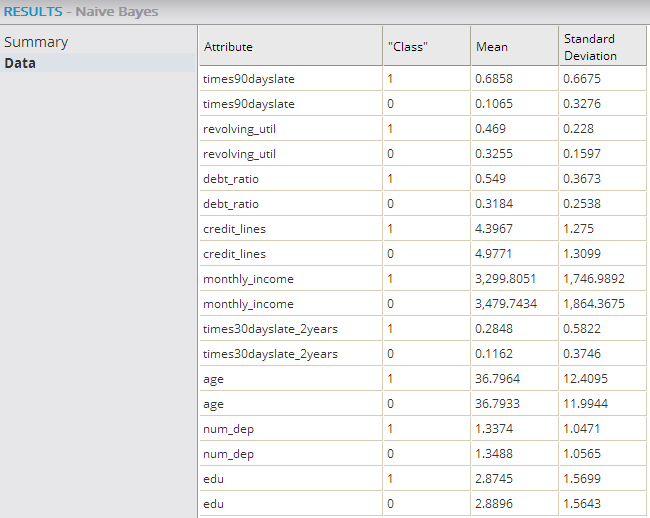
- Data Results
- The
Data results display calculated standard deviation curve fit numbers (Means and Standard Deviations) for each independent variable (per dependent variable outcome) in the model.
- Data Output
- Naive Bayes model. When creating a Naive Bayes model, the modeler should add Model Validation Operators1 to get further Naive Bayes model accuracy statistics (from the Goodness of Fit Operator) and/or visual outputs (from the ROC and Lift Operators). The ROC Curve in particular is a useful visual tool for comparing classification models.

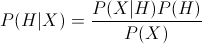 , where
, where