Alpine Forest Regression
Applies an ensemble algorithm to make a numerical prediction by aggregating (majority vote or averaging) the numerical regression tree predictions of the ensemble.
Configuration
| Parameter | Description |
|---|---|
| Notes | Any notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk is displayed on the operator. |
| Dependent Column |
The quantity to model or predict.
A Dependent Column must be specified for Alpine Forest. Select the data column to be considered the Dependent Variable for the classification. |
| Columns | Allows you to select the Independent Variable data columns to include for the decision tree training. |
| Number of Trees | Specifies how many individual decision trees to train in the Alpine Forest Regression. Increasing the number of trees created generally increases the accuracy of the model. However, as long as enough trees are created, the Alpine Forest Regression model is not very sensitive to changing this parameter.
Note: The user interface only displays a maximum of 20 tree results, even if more are generated internally.
Default value: 10. |
| Use Automatic Configuration | Allows
Team Studio to determine all the required Alpine Forest configuration parameters except for the
Number of Trees parameter.
Default value: true. |
| Number of Features Function | Automatically determines the
Number of Features per Node parameter.
Options:
Default value: Square Root. |
| Number of Features per Node | Specifies
m, the number of predictors to consider at each node during tree building process. The Alpine Forest algorithm calculates the best split for the tree based on these
m variables that are selected randomly from the training set.
Number of Features per Node should be much less than the number of columns specified for the Columns property. Note: Number of Features per Node is the main configuration parameter to which an Alpine Forest model is most sensitive. Increasing the variable number per split makes each of the Decision Trees bigger, providing more information at each node. However, it also becomes harder to interpret for the modeler.
Default value: 1 (for Hadoop). |
| Sampling with Replacement |
Specifies whether to use replacement when selecting training variable data row samples from the input data set. This property controls whether a data row can be reused for each of the n training data samples collected from the available data set rows.
|
| Sampling Percentage (-1=Automatic) | Specifies the fraction of overall data rows available to select for the random sample data rows used for each decision tree.
Caution: If
Sampling Percentage is set too large for Hadoop, the number of samples might be larger than what an individual tree trainer can fit in memory (which is determined in Hadoop by
Max JVM Heap Size). In this case,
Team Studio drops random samples so that eventually all training samples can fit in memory.
|
| Max Depth (-1=Unlimited) | Sets the "depth" of the tree or the maximum number of decision nodes it can branch out to beneath the root node during the tree-growth phase. A tree stops growing any deeper if either a node becomes empty (that is, there are no more examples to split in the current node) or the depth of the tree exceeds this
Max Depth limit.
Default value: 5. |
| Min Size For Split | (Pre-pruning parameter)
Specifies the minimal size (or number of members) of a node in the decision tree in order to allow a further split. If the node has fewer data members than the Minimal Size for Split, it must become a leaf or end node in the tree. When individual trees are being trained, this is a criteria for stopping tree training. Minimal Size for Split is referenced during the pre-pruning phase. Default value: 2. |
| Min Leaf Size | (Pre-pruning parameter)
Limits the tree depth based on the size of the leaf nodes, ensuring enough data makes it to each part of the tree. This is useful when the model construction is taking too long or when the model shows very good ROC on training data but not nearly as good performance on hold-out or cross-validation data (due to over-fitting). For example, if the Min Leaf Size is 2, each terminal leaf node must contain at least 2 training data points. The range of possible values is any integer value ≥ 1. Default value: 1. |
| Max JVM Heap Size (MB) (-1=Automatic) | The
Max JVM Heap Size (for Hadoop only) determines the amount of virtual memory assigned to an individual tree trainer. The number of training samples for a single tree is limited by this.
Default value: 1024. A value of -1 automatically sets the Max JVM Heap Size to avoid out-of-memory issues. |
| Use Spark | If Yes (the default), uses Spark to optimize calculation time. |
| Advanced Spark Settings Automatic Optimization |
|
Output
- Visual Output
-
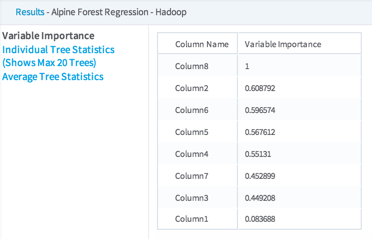
Variable Importance - The results provide the Regression Coefficient values for each independent variable in the model.
At each split, we calculate how much this split reduces node impurity (purity gain). Then for each variable, we sum up over all splits where it is used (weighted by the number of samples used in the node), over all trees. We then find the variable that has the maximum purity gain and divide by this value across all variables.
For Alpine Forest Regression, we use Variance Reduction as the impurity function.

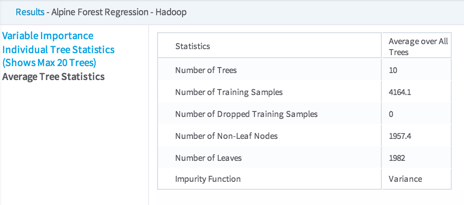
Individual Tree Statistics - Shows the results for each Decision Tree in the model, up to a maximum of 20 trees.
- Data Output
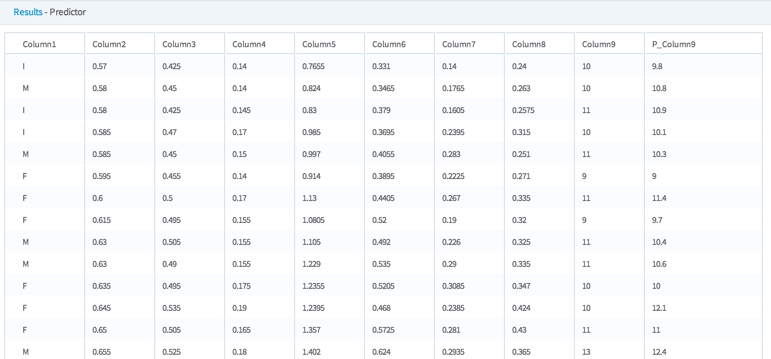
- Typically, an Alpine Forest Regression model is followed by a Predictor operator which provides the prediction value for each data row compared against the actual data set training value and the associated confidence level.
Note: Currently, the Alpine Forest Regression operator does not have a specific Evaluator operator for it. Use the Predictor operator to compare predicted versus actual values and generally assess the accuracy of the Alpine Forest Regression operator .
The following illustration shows output from the Predictor operator for the Alpine Forest Regression operator.
The P_ column can be compared to the actual values of the dependent column (in this case Column9) in order to assess the accuracy of the model.