PCA (HD)

Uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables (principal components).

Information at a Glance

Category	Model
Data source type	HD
Sends output to other operators	Yes
Data processing tool	MapReduce

Algorithm

PCA (Principal Component Analysis) is an orthogonal linear transformation that transforms data into a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, the third on the third coordinate, continuing until the number of rows has been reached or a preset maximum principal component threshold has been reached.

The Alpine PCA operator implements an eigenvalue decomposition of a data covariance matrix Σ (or, correlation matrix R).

Each principal component is a linear combination of the original variables.
The coefficients (loadings) are the eigenvectors (v1, v2,...vp) of covariance matrix Σ (or, correlation matrix R) with unit length.
The eigenvalues (λ1, λ2,...λp) denote the contribution of the principal component associated with it.
The principal components are sorted by descending order according to their variance contribution.
The user can choose the number of principal components according to the accumulation contribution (∑ij=1λj/∑pK=1λK).

More details are available in Principal Component Analysis, (1986), Joliffe, I.T.

Additional references:

Jerome Friedman, Trevor Hastie, Robert Tibshirani (2008), The Elements of Statistical Learning Data Mining, Inference and Prediction Chapter 3: "Linear Methods for Regression"
Joliffe, I.T. (1986), Principal Component Analysis, New York, Springer
Wu, W., Massart, D.L., and de Jong, S. (1997), "The Kernel PCA Algorithms for Wide Data. Part I: Theory and Algorithms" Chemometrics and Intelligent Laboratory Systems, 36, 165-172.

Input

A data set from the preceding operator.

Configuration

Parameter	Description
Notes	Schema where MADlib is installed in the database. MADlib must be installed in the same database as the input dataset. If a "madlib" schema exists in the database, this parameter defaults to madlib.
Columns	Click Columns to open the dialog box for selecting the available variable columns to transform by the PCA algorithm, in order to create a reduced set of variables.
Center	If Yes (the default), the mean value of each variable column is set to 0 before the PCA matrix transformation algorithm is run. In combination with Scale, the following applies. If Yes, and Scale is No, then a Covariance matrix is applied. If Yes, and Scale is Yes, then a Correlation matrix is applied. If No, and Scale is No, then an uncorrected covariance matrix is applied. Usually, the PCA algorithm has meaning only if the data is centered first, so the default is set to Yes.
Scale	When the Scale option is selected, each variable's data values are divided by the Standard Deviation in order for all the columns to have the same data spread (that is, be on an equivalent scale as each other). See Center for more information about its effect on the algorithm. Default value: No. (In some cases, scaling is not desirable.)
In Memory Threshold	Determines whether to compute the PCA by a Hadoop MapReduce job or in memory SVD (single machine instead of distributed mode). If the number of rows in the training data set is fewer than the threshold value, the PCA algorithm is run in memory SVD. Otherwise, it is computed by a MapReduce job.
Maximum Rank for Distributed Mode	Determines the upper-limit number of principal components to calculate, starting with the top, high-ranking variance components. This value must be equal to or typically less than the number of columns in the training data set, to help with dimension reduction.
Additional Runs for Distributed Mode	Specifies the number of required extra passes of the algorithm to implement when computing in-memory SVD. Typically, a single pass result is sufficient when the number or rows are less than the In Memory Threshold value. Default value: 0 (no additional runs).
Max JVM Heap Size (MB) (-1=Automatic)	A Java Virtual Machine data storage setting for Hadoop. The default value is 1024. If the value is -1, the system sets the heap size automatically.

Output

Visual Output

The visual output for Hadoop provides visualizations of the principal components and their contribution weightings, scaling, centering, variance, and cumulative variance.

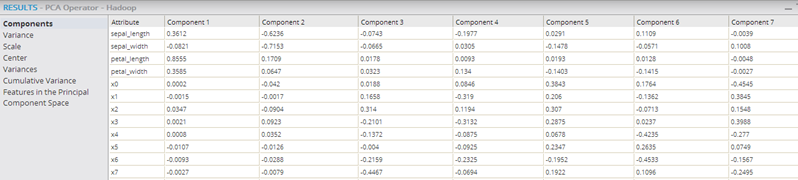
Components: Shows the new principal components as the columns and each row provides the source data variable's contribution to the derived component value.
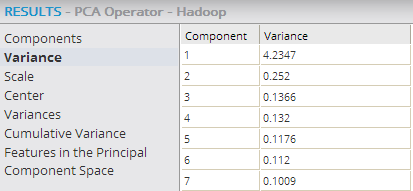
Variance: Shows each principal component's contribution to the overall data variance. Variance provides a measure of how much of all the variance in the original data set is captured by a given component.
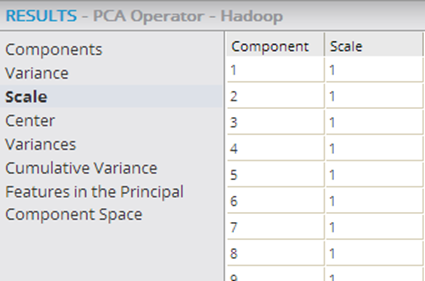
Scale: Shows the relative size of the source data set's columns relative to their original values passed in. Note: if the value is not "1" (meaning 100% of its original value), no scaling was done prior to running the PCA algorithm.
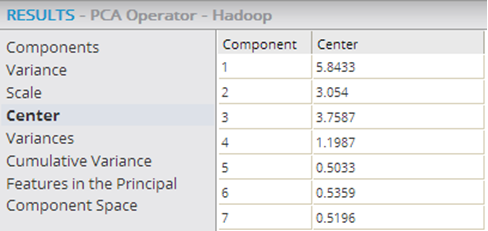
Center: Shows if any centering was done to the original data set column to clean up the data before computing the principal components. The data displayed shows the center value of the original data set's columns that were used in the PCA algorithm. Note: If the values are not 0, the data was not centered prior to running the algorithm. It is best to normalize the source data and center it around 0 before running the PCA algorithm.
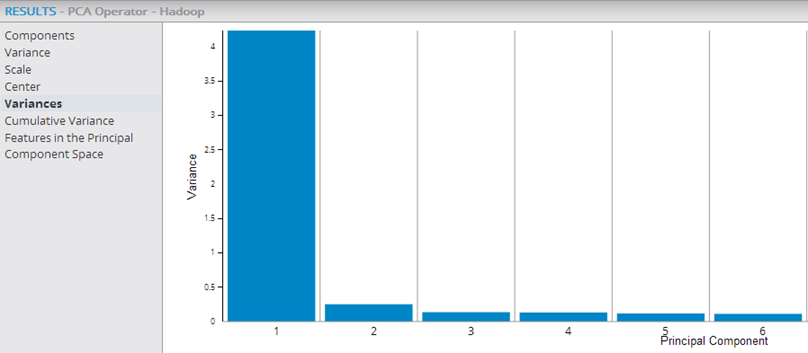
Variances: Shows each principal component's contribution to the overall data variance (for the Variance data provided above). Variance provides a measure of how much of all the variance in the original data set is captured by a given component. The visualization output is helpful to quickly see how many of the principal components explain most of the data set's variance. If the first few principal components have higher Variance values and then the values drop off, those are the components that should be used as the reduced dimension data set.
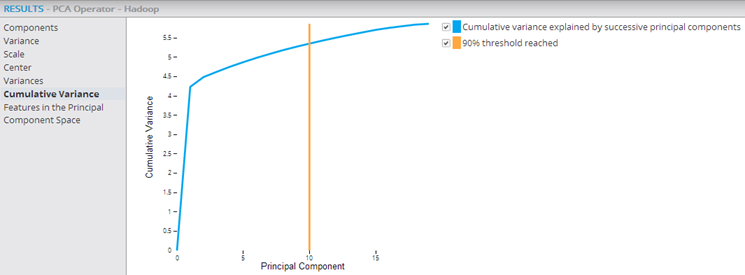
Cumulative Variance: This graph provides a visualization of the cumulative importance of each principal component (starting with the most significant principal component) and of how effectively the components explain the data set. The 90% Threshold Reached line shows the cumulative principal component point at which 90% of the data variance is explained. This helps know how many of the principal components explain the bulk of the data variance. In the example below, it is the first 10 principal components that explain 90% of the data variance.
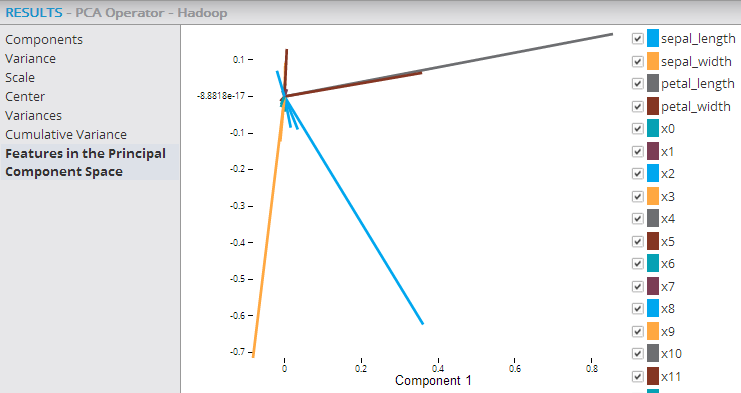
Features in the Principal Component Space: This graph provides a visualization of the source variables' (columns) axis from the original data space into the two-dimensional space spanned by the first and second principal components. As a result, those variables (columns) whose axes are near each other in the Principal component space have higher correlation to each other and the longer vectors (axes) have higher relevance in explaining the overall variance. In the example below, the three axes for sepal_width, sepal_length, and petal_length are the longest and most relevant to the datavariance. Also, the sepal_width and sepal_length variables are more closely correlated to each other than the sepal_length and petal_length are.

Note: To learn more about the visualization available in this operator, go to Explore Visual Results.

Data Output

The PCA Operator for Hadoop outputs the matrix transformation algorithm (not the transformed, reduced data set itself).

Note: To perform the transformation against a data set, the Hadoop PCA operator must be succeeded by a PCA Apply operator. The transformation can then be processed against the source training data set or a new input data set (with the same variables).

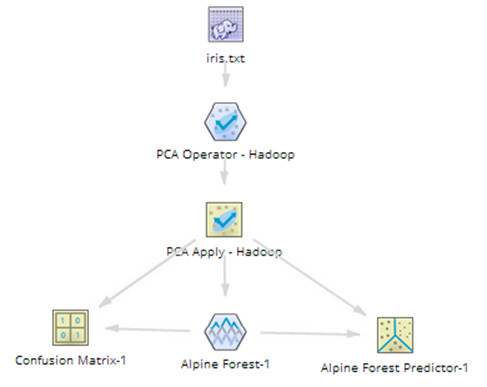
The following example shows the PCA and PCA Apply operators within a Hadoop workflow, with their output being passed into an Alpine Forest model.

See the PCA Apply operator for more details.

Contents

Index