Linear Regression - MADlib

Team Studio supports the MADlib open source implementation of the Linear Regression algorithm.

Information at a Glance

Category Model
Data source type DB
Sends output to other operators No
Data processing tool MADlib

Algorithm

The MADlib Linear Regression operator applies an Ordinary Least-Squares (OLS) linear regression algorithm to the input dataset. It is processed using the least squares method of regression analysis, meaning that the model is fit such that the sum-of-squares of differences of observed and predicted values is minimized.

More information including general principles can be found in the official MADlib documentation.

Input

A data set that contains the dependent and independent variables for modeling.

Configuration

Parameter Description
Notes Any notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk is displayed on the operator.
MADlib Schema Name Schema where MADlib is installed in the database. MADlib must be installed in the same database as the input dataset. If a "madlib" schema exists in the database, this parameter defaults to madlib.
Model Output Schema Name The name of the schema where the output is stored.
Model Output Table Name The name of the table that is created to store the Regression model. Specifically, the model output table stores:

[ group_col_1 | group_col_2 | ... |] coef | r2 | std_err | t_stats | p_values | condition_no [| bp_stats | bp_p_value]

See the official MADlib linear regression documentation for more information.

Drop If Exists
  • If Yes (the default), drop the existing table of the same name and create a new one.
  • If No, stop the flow and alert the user that an error has occurred.
Dependent Variable Required. The quantity to model or predict.
  • The list of the available columns is displayed. Select the data column to be considered the Dependent Variable for the regression.
  • The Dependent Variable should be a numerical data type.
Independent Variables Click Select Columns to select the available columns from the input data set for analysis.

Select the independent variable data columns for the regression analysis or model training.

You must select at least one column.

Grouping Columns You can set at least one column to group the input data and build separate regression models for each group.

Click Select Columns to open the dialog box for selecting the available columns from the input dataset for grouping.

Heteroskedacity Stat Set to true (the default) to output two additional columns to the model table.
  • Breusch-Pagan test statistics (bp_stats)
  • the corresponding p-value (bp_p_value)
Draw Residual Plot Set to true (the default) to output Q-Q Plot and Residual Plot graphs for the linear regression results.
  • The Q-Q Plot graphically compares the distribution of the residuals of a given variable to the normal distribution (represented by a straight line).
  • The Residual Plot displays a graph that shows the residuals of a linear regression model on the vertical axis and the independent variable on the horizontal axis.

Output

When assessing the Data tab results of the Linear Regression Operator, a modeler focuses mostly the Coefficient values, which indicate the strength of the effect of the independent variables on the dependent variable, and the associated P-values, which indicate how much not to trust the estimated correlation measurement.

Visual Output
The MADlib Linear Regression Operator results output is displayed across the Summary and Data sections.
Summary

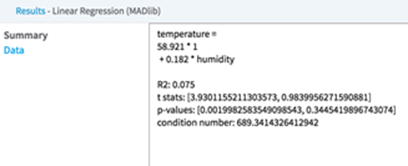
The derived linear regression model is a mathematical equation linking the Dependent Variable (Y) to the Independent Variables (X1, X2, etc.). It includes the scaling or Coefficient values (β1, β2, etc.) associated with each independent variable in the model. Note: The resulting linear equation is expressed in the form of Y= β0 + β1*X1 + β2*X2 + …

The following overall model statistical fit numbers:

  • R2: R2 is called the multiple correlation coefficient of the model, or the Coefficient of Multiple Determination. It represents the fraction of the total Dependent Variable (Y) variance explained by the regression analysis, with 0 meaning 0% explanation of Y variance and 1 meaning 100% accurate fit or prediction capability.
    Note: In general, an R2 value greater than .8 is considered a good model. However, this value is relative and in some situations just getting an improved R2 from .5 to .6, for example, would be beneficial.
  • S: represents the standard error per model (often also denoted by SE). It is a measure of the average amount that the regression model equation over- or under-predicts.
    • The rule of thumb data scientists use is that 60% of the model predictions are within /- 1 SE and 90% are within /- 2 SEs.

For example, if a linear regression model predicts the quality of the wine on a scale between 1 and 10 and the SE is .6 per model prediction, then a prediction of Quality=8 means the true value is 90% likely to be within 2*.6 of the predicted 8 value (that is, the real Quality value is likely between 6.8 and 9.2).

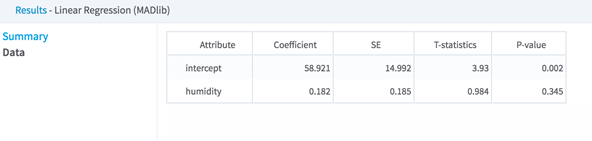
Note: The higher the R2 and the lower the SE, the more accurate the linear regression model predictions are likely to be.



Data
Displays the model coefficients and statistical fit numbers for each Independent variable in the model.

Column Description
Coefficient The model coefficient, β, indicates the strength of the effect of the associated independent variable on the dependent variable.

Standard Error, or SE, represents the standard deviation of the estimated Coefficient values from the actual Coefficient values for the set of Variables in the regression.

  • It is best practice to commonly expect + or - 2 Standard Errors, meaning the actual Coefficient value should be within 2 SEs of the estimate.
  • Therefore, a modeler looks for the SE values to be much smaller than the associated forecasted Coefficient values.
T-statistic The T-statistic is computed by dividing the estimated value of the β Coefficient by its Standard Error, as follows: T= β/SE. It provides a scale for how big of an error the estimated coefficient has.
  • A small T-statistic alerts the modeler to the fact that the error is almost as big as the Coefficient measurement and is therefore suspicious.
  • The larger the absolute value of T, the less likely that the unknown actual value of the Coefficient could be zero.1
P-value P-value represents the probability of still observing the dependent variable's value if the Coefficient value for the independent variable is zero (that is, if p-value is high then the associated variable would not be considered relevant as a correlated, independent variable in the model).
  • A low P-value is evidence that the estimated Coefficient is not due to measurement error or coincidence, and therefore, is more likely a significant result. Thus, a low P-value gives the modeler confidence in the significance of the variable in the model.
  • Standard practice is to not trust Coefficients with P-values greater than 0.05 (5%). Note: a P-value of less than 0.05 is often conceptualized as there being over 95% certainty that the Coefficient is relevant.2
    Note: The smaller the P-value, the more meaningful the coefficient or the more certainty over the significance of the independent variable in the Linear Regression model.
Data Output
None. This is a terminal operator.
Related reference