Stepwise Model Builder Overview
The purpose of the Statistica Stepwise Model Builder module is to facilitate the identification of logistic regression models (see also Generalized Linear/Nonlinear Models) based on predictors chosen by the user at each step. The final logistic regression model can then be saved in XML/PMML form or directly deployed to Stastica Enterprise as a prediction (scoring model), for example to be referenced in the Decisioning Platform.
The module will compute continuous and categorical predictors with multiple degrees of freedom, and automatically move the latter into/out of the regression equation in single steps.
At each step, the program will compute various predictor statistics for predictors in the current model, and predictors (predictor candidates) not in the current equation. Statistics reflecting on the overall model quality are also computed.
Thus, you can build models by manually selecting the most important predictors into the regression equation one step at a time, using criteria of statistical significance for the prediction as well as policy and other criteria. By moving selected variables or groups of variables into the prediction and equation, and removing others from that equation, what-if (scenario) analyses are possible to assess the impact of certain model assumptions, policy, or regulatory constraints (for example, on predictors that are not permitted). Thus, analysts can build models that are parsimonious, consistent with policies, guidelines, and regulatory constraints, but are also as accurate as possible.
Logistic Regression
Logistic Regression for modeling binary outcome variables – such as credit default or insurance or warranty claim incidences – is described in detail in the Statistica Generalized Linear/Nonlinear Models Help topics; see also Logit Regression and Transformation in the Glossary. In short, in logit regression, a linear model of predictors is used to predict the logit-transformed probabilities of observations belonging to one of two classes.
The regression model can be expressed as:
Where p(y=1) is the probability of the event of interest, for example, credit default, warranty or insurance claim, and so on; and where b0 + b1*x1+…+bn*xn is the linear equation in the predictor or x variables.
Stepwise Predictor Selection
In many applications, it is desirable or required to strictly control the nature of the predictor variables that are used for predicting certain outcomes. For example, in the credit scoring domain, in the US it is customarily not permitted to use variables associated with the ethnicity or race of an applicant. Also, domain experts usually bring to the modeling task significant prior knowledge about which predictors are most diagnostic for the prediction of interest.
In both cases, it is essential that the analyst can manually select the variables of interest, and avoid variables that are not permissible or desirable.
Subsampling for Responsive Marginal Analyses
Computationally, during the analyses at each step, the program will estimate the logistic regression model of all predictors currently in the equation, adding and then removing each predictor not in the equation, one by one. Thus, if there are, for example, 100 predictors that are to be evaluated at a particular step in the model building process, then 100 regression equations will have to be estimated in order to derive information about the added diagnostic value – or marginal utility – and “quality” of each of those predictors.
In order to speed up computations, it is often useful to apply sampling to this process. Recall that the accuracy of statistical parameters describing a population is a function of the sample size from which the parameters are computed, and not the population size itself. This means that parameter estimates for a 5-predictor logistic regression model estimated in a sample of, say, 6,000 observations is as accurate for a population of 10,000 cases as it is for a population of 10,000,000 cases. Therefore, it usually makes little sense to estimate the predictor statistics in the full data set when that data set is many times larger than the number of parameters that are to be estimated.
In the Stepwise Model Builder module, there are options that allow analysts to estimate the parameters in the marginal analyses (predictor statistics for predictors currently not in the regression equation) based on a subsample of cases only. This usually speeds up computations dramatically when evaluating large predictor sets (many predictors). Of course, the final regression equation is always computed from all cases.
In practice, a sample of at least 40 times as many observations as parameters in the current equation is usually desirable, although the quality of the marginal results from a sample (how close they are to the results computed from all observations) will also depend on the distribution of the binary outcome variable of interest. For example, when predicting very rare cases (for example, credit default with a very low base rate in the population), it is usually advisable to perform the stepwise model building on all cases.
Re-estimating marginal results. Note that the Stepwise Model Builder module provides options for analysts to re-estimate marginal results for selected predictors, based on the full set of observations rather than only a subset. In this manner, an analyst can first perform very quick screening of predictor candidates, and then more closely review results for selected variables by repeating the marginal analyses using all cases.
Sampling, Bootstrapping
Typically, model building is performed on a subsample of all the cases available for modeling in the respective business unit, department, and so on. As described above, there is no reason to build models based on all customers available to a bank or all policies at an insurer. Properly drawn samples for modeling will provide results of effectively the same precision and quality as those computed from the cases in the entire population. More importantly, by “reserving the opportunity” to go back to the original databases to select another validation sample, analysts can assess the predictive accuracy of their models against cases that were not considered during the model building process. In practically all data mining and predictive modeling, it is customary to split the data into learning and testing samples so that the predictive accuracy of models can be assessed by scoring one or more samples of observations that were never considered by analysts during modeling.
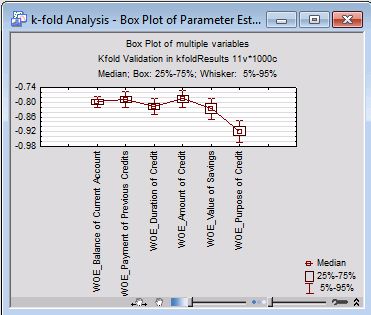
Another method to gage the robustness of models and the parameters in the model, as well as the predictions made by the model, is to re-estimate the model statistics of interest such as parameter estimates, goodness-of-fit indices, predictions in a hold-out sample, and so on, while repeatedly resampling from the data. The Bootstrap capabilities in the Stepwise Model Builder module provide such options to repeat k times the parameter estimation on data sets of the same size obtained by sampling with replacement from the original data. In each repetition, a hold-out sample can also be designated for estimating predictive accuracy in a hold-out sample (in each replication).
For example, we might repeat the estimation procedure (with or without hold-out sample) 1,000 times for data created via sampling with replacement from the original data set. As a result, we will obtain a distribution of parameter estimates for each parameter over the 1,000 replications, as well as the distributions for all other relevant statistics.
Those distributions can then be plotted and further analyzed to identify parameters that are less robust (show a great deal of variability over the replications), or that, for example, in a significant number of replications are very close to 0 (contribute nothing to the prediction equation).
Deployment of Models
The Stepwise Model Builder module is an integral part of the Statistica Decisioning Platform and solution. Specifically, the models generated by this module, as well as any other predictive or data mining model for classification or regression prediction, can be referenced in the Rules node of the Decisioning Platform, and define the scoring or conditional scoring of new observations.
Because models are managed as reusable templates (objects) in the Enterprise platform that can be referenced by the Rules nodes in Decisioning flows, model changes will automatically propagate to all places where they are used (referenced).