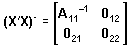Generalized Linear Model (GLM) Introductory Overview - Extension of Multiple Regression to the General Linear Model
One way in which the general linear model differs from the multiple regression model is in terms of the number of dependent variables that can be analyzed. The Y vector of n observations of a single Y variable can be replaced by a Y matrix of n observations of m different Y variables. Similarly, the b vector of regression coefficients for a single Y variable can be replaced by a b matrix of regression coefficients, with one vector of b coefficients for each of the m dependent variables. These substitutions yield what is sometimes called the multivariate regression model, but it should be emphasized that the matrix formulations of the multiple and multivariate regression models are identical, except for the number of columns in the Y and b matrices. The method for solving for the b coefficients is also identical, that is, m different sets of regression coefficients are separately found for the m different dependent variables in the multivariate regression model.
The general linear model goes a step beyond the multivariate regression model by allowing for linear transformations or linear combinations of multiple dependent variables. This extension gives the general linear model important advantages over the multiple and the so-called multivariate regression models, both of which are inherently univariate (single dependent variable) methods. One advantage is that multivariate tests of significance can be employed when responses on multiple dependent variables are correlated. Separate univariate tests of significance for correlated dependent variables are not independent and may not be appropriate. Multivariate tests of significance of independent linear combinations of multiple dependent variables also can give insight into which dimensions of the response variables are, and are not, related to the predictor variables. Another advantage is the ability to analyze effects of repeated measure factors. Repeated measure designs, or within-subject designs, have traditionally been analyzed using ANOVA techniques. Linear combinations of responses reflecting a repeated measure effect (for example, the difference of responses on a measure under differing conditions) can be constructed and tested for significance using either the univariate or multivariate approach to analyzing repeated measures in the general linear model.
A second important way in which the general linear model differs from the multiple regression model is in its ability to provide a solution for the normal equations when the X variables are not linearly independent and the inverse of X'X does not exist. Redundancy of the X variables may be incidental (e.g., two predictor variables might happen to be perfectly correlated in a small data set), accidental (e.g., two copies of the same variable might unintentionally be used in an analysis) or designed (e.g., indicator variables with exactly opposite values might be used in the analysis, as when both Male and Female predictor variables are used in representing Gender). Finding the regular inverse of a non-full-rank matrix is reminiscent of the problem of finding the reciprocal of 0 in ordinary arithmetic. No such inverse or reciprocal exists because division by 0 is not permitted. This problem is solved in the general linear model by using a generalized inverse of the X'X matrix in solving the normal equations. A generalized inverse is any matrix that satisfies
AA`A = A
for a matrix A.
A generalized inverse is unique and is the same as the regular inverse only if the matrix A is full rank. A generalized inverse for a non-full-rank matrix can be computed by the simple expedient of zeroing the elements in redundant rows and columns of the matrix. Suppose that an X'X matrix with r non-redundant columns is partitioned as
where A11 is an r by r matrix of rank r. Then the regular inverse of A11 exists and a generalized inverse of X'X is
where each 0 (null) matrix is a matrix of 0's (zeroes) and has the same dimensions as the corresponding A matrix.
In practice, however, a particular generalized inverse of X'X for finding a solution to the normal equations is usually computed using the sweep operator (Dempster, 1960). This generalized inverse, called a g2 inverse, has the important property that partitioning or reordering of the columns of X'X is unnecessary, so that the matrix can be inverted "in place."
There are infinitely many generalized inverses of a non-full-rank X'X matrix, and thus, infinitely many solutions to the normal equations. This can make it difficult to understand the nature of the relationships of the predictor variables to responses on the dependent variables, because the regression coefficients can change depending on the particular generalized inverse chosen for solving the normal equations. It is not cause for dismay, however, because of the invariance properties of many results obtained using the general linear model.
A simple example may be useful for illustrating one of the most important invariance properties of the use of generalized inverses in the general linear model. If both Male and Female predictor variables with exactly opposite values are used in an analysis to represent Gender, it is essentially arbitrary as to which predictor variable is considered to be redundant (e.g., Male can be considered to be redundant with Female, or vice versa). No matter which predictor variable is considered to be redundant, no matter which corresponding generalized inverse is used in solving the normal equations, and no matter which resulting regression equation is used for computing predicted values on the dependent variables, the predicted values and the corresponding residuals for males and females will be unchanged. In using the general linear model, one must keep in mind that finding a particular arbitrary solution to the normal equations is primarily a means to the end of accounting for responses on the dependent variables, and not necessarily an end in itself.
Other GLM Introductory Overview Topics
A detailed discussion of univariate and multivariate ANOVA techniques can also be found in Introductory Overview section of the ANOVA/MANOVA module; a discussion of multiple regression methods is provided in the Multiple Regression Overviews.