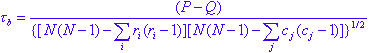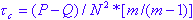Statistics in Crosstabulations - Statistics Based on Ranks
In many cases the categories used in the crosstabulation contain meaningful rank-ordering information; that is, they measure some characteristic on an ordinal scale.
Suppose we asked a sample of respondents to indicate their interest in watching different sports on a 4-point scale with the explicit labels (1) always, (2) usually, (3) sometimes, and (4) never interested. Obviously, we can assume that the response sometimes interested is indicative of less interest than always interested, and so on. Thus, we could rank the respondents with regard to their expressed interest in, for example, watching football. When categorical variables can be interpreted in this manner, there are several additional indices that can be computed to express the relationship between variables.
Statistics Based on Ranks - Spearman R
Spearman R can be thought of as the regular Pearson product-moment correlation coefficient (Pearson r); that is, in terms of the proportion of variability accounted for, except that Spearman R is computed from ranks. As mentioned above, Spearman R assumes that the variables under consideration were measured on at least an ordinal (rank order) scale; that is, the individual observations (cases) can be ranked into two ordered series. Detailed discussions of the Spearman R statistic, its power and efficiency can be found in Gibbons (1985), Hays (1981), McNemar (1969), Siegel (1956), Siegel and Castellan (1988), Kendall (1948), Olds (1949), or Hotelling and Pabst (1936).
Statistics Based on Ranks - Kendall's Tau
Kendall's tau-b is computed as:
tau-b = (# agreements - # disagreements) / total number of pairs
where P and Q are the number of concordant pairs (# agreements) and discordant pairs (# disagreements), respectively.
For small n (n <10), the exact probability can be calculated. The tabulated values can be found in Siegel and Castellan. However, the exact sampling distribution of tau approaches a normal distribution very quickly with increasing n size. For n = 10 or more, refer to the normal distribution (Hays, 1988).
Kendall's tau is equivalent to the Spearman R statistic with regard to the underlying assumptions. It is also comparable in terms of its statistical power. However, Spearman R and Kendall's tau are usually not identical in magnitude because their underlying logic, as well as their computational formulas, are very different. Siegel and Castellan (1988) express the relationship of the two measures in terms of the inequality:
-1 <= 3 * Kendall's tau - 2 * Spearman R <= 1
More importantly, Kendall's tau and Spearman R imply different interpretations: While Spearman R can be thought of as the regular Pearson product-moment correlation coefficient as computed from ranks, Kendall's tau rather represents a probability. Specifically, it is the difference between the probability that the observed data are in the same order for the two variables versus the probability that the observed data are in different orders for the two variables. Kendall (1948, 1975), Everitt (1977), and Siegel and Castellan (1988) discuss Kendall's tau in greater detail.
where m = min(R,C).
Stuart's tau-c makes a correction for table size in addition to a correction for ties. In most cases these values will be fairly similar, and when discrepancies occur, it is probably always safest to interpret the lowest value.
Statistics Based on Ranks - Somers' D: d(X|Y), d(Y|X)
Somers' D is an asymmetric measure of association related to tb (see Siegel & Castellan, 1988, p. 303-310).
Statistics Based on Ranks - Gamma
The Gamma statistic is preferable to Spearman R or Kendall tau when the data contain many tied observations. In terms of the underlying assumptions, Gamma is equivalent to Spearman R or Kendall tau. In terms of its interpretation and computation, it is more similar to Kendall tau than Spearman R. In short, Gamma is also a probability; specifically, it is computed as the difference between the probability that the rank ordering of the two variables agree minus the probability that they disagree, divided by 1 minus the probability of ties. Thus, Gamma is basically equivalent to Kendall tau, except that ties are explicitly taken into account.
Detailed discussions of the Gamma statistic can be found in Goodman and Kruskal (1954, 1959, 1963, 1972), Siegel (1956), and Siegel and Castellan (1988).
Statistics Based on Ranks - Uncertainty Coefficients
These are indices of stochastic dependence; the concept of stochastic dependence is derived from the information theory approach to the analysis of frequency tables. For more information, refer to the appropriate references (see Kullback, 1959; Ku & Kullback, 1968; Ku, Varner, & Kullback, 1971; see also Bishop, Fienberg, & Holland, 1975, p. 344-348). S(Y,X) refers to symmetrical dependence, S(X|Y) and S(Y|X) refer to asymmetrical dependence.