Elastic Net Logistic - MADlib
Team Studio supports the MADlib implementation of the Elastic Net Logistic Regression algorithm.
Algorithm
This module implements elastic net regularization for logistic regression problems. Elastic net regularization seeks to find a weight vector that, for any given training example set, minimizes a metric function that combines the L1 and L2 penalties of the lasso and ridge regression methods.
For more information, including general principles, see the official MADlib documentation.
Input
A database data set that contains the dependent and independent variables for modeling. The data set must have at least one Boolean column and at least one numeric type column.
Configuration
| Parameter | Description |
|---|---|
| Notes | Any notes or helpful information about this operator's parameter settings. When you enter content in the Notes field, a yellow asterisk is displayed on the operator. |
| MADLib Schema Name | The schema where MADlib is installed in the database. MADlib must be installed in the same database as the input data set. If a "madlib" schema exists in the database, this parameter defaults to madlib. |
| Model Output Schema Name | The name of the model output schema. |
| Model Output Table Name |
The name of the table that is created to store the regression model.
The model output table stores the following. family | features | features_selected | coef_nonzero | coef_all | intercept | log_likelihood | standardize | iteration_runSee the official MADlib elastic net regularization documentation for more information. |
| Drop If Exists | |
| Dependent Variable | The quantity to model or predict. This must be a Boolean column. The list of the available data columns for the Elastic Net Logistic operator is displayed. Select the data column to be considered the dependent variable for the regression. |
| Independent Variables |
Select the data columns to include for the regression analysis or model training. At least one column or one interaction must be specified.
Click Select Columns to open the dialog box for selecting the available columns from the input data set for analysis. |
| Control Parameter | The elastic net Control Parameter (alpha) must be a value in [0,1]. |
| Regularization Parameter | The Regularization Parameter (lambda) must be a positive value. |
| Standardize | A Boolean flag that specifies the option to normalize the data. The default value is true, which often yields better results and faster convergence. |
| Optimizer | Can be fista (Fast Iterative Shrinkage-Thresholding Algorithm) or igd (Incremental Gradient Descent). The required proceeding optimizer configuration parameters are dependent on the optimizer selected.
See the official MADlib elastic net regularization documentation for more information. |
| FISTA Maximum Stepsize | The initial backtracking step size. At each iteration, the algorithm first tries
stepsize = max_stepsize , and if it does not work, it tries a smaller step size,
stepsize = stepsize/eta, where eta must be larger than 1. At first glance, this seems to perform repeated iterations for even one step, but using a larger step size actually greatly increases the computation speed and minimizes the total number of iterations. A careful choice of
max_stepsize can decrease the computation time by more than 10 times.
Default value: 4.0. |
| FISTA Eta | If
stepsize does not work,
stepsize /eta is tried. This value must be greater than 1.
Default value: 2.0. |
| Warmup |
|
| Warmup Lambdas | The lambda value series to use when warmup is true. The default is NULL, which means that lambda values are automatically generated. |
| Number of Warmup Lambdas | The number of lambdas used in warmup. If
warmup_lambdas is not
NULL, this value is overridden by the number of provided lambda values.
Default value: 15. |
| Warmup Tolerance | The value of tolerance used during warmup. Default value: 1e-6. |
| FISTA Use Active Method |
|
| FISTA Active Tolerance | The value of tolerance used during active set calculation. Default value: 1e-6. |
| FISTA Random Step Size | Specify whether to add some randomness to the step size. Sometimes, this can speed up the calculation. Default value: 1e-6. |
| IGD Step Size | The initial backtracking step size. Default value: 0.01. |
| IGD Zero Coefficient Threshold | When a coefficient is very small, set this coefficient to
0. Due to the stochastic nature of SGD, we can only obtain very small values for the fitting coefficients. Therefore, threshold is needed at the end of the computation to screen out tiny values and hard-set them to zeros. This is accomplished as follows.
Default value: 1e-10. |
| IGD Paralellize | Specify whether to run the computation on multiple segments. SGD is a sequential algorithm in nature. When running in a distributed manner, each segment of the data runs its own SGD model and then the models are averaged to get a model for each iteration. This averaging might slow down the convergence speed, although we also acquire the ability to process large data sets on multiple machines. This algorithm, therefore, provides the parallel option to allow you to choose whether to do parallel computation.
Default value: true. |
| Maximum Iterations | When the difference between coefficients of two consecutive iterations is smaller than the convergence tolerance or the iteration number is larger than
Maximum Iterations, the computation stops.
Default value: 10000. |
| Convergence Tolerance | When the difference between coefficients of two consecutive iterations is smaller than the
Convergence Tolerance or the iteration number is larger than Maximum Iterations, the computation stops.
Default value: 1e-6. |
Output
- Visual Output
-
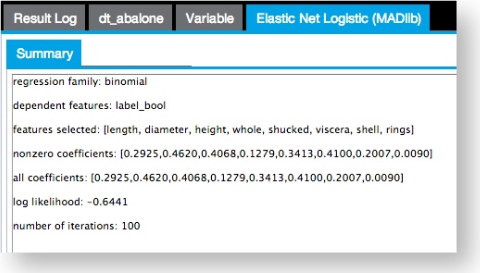
Output is displayed on the Summary tab, which displays the features selected, non-zero coefficients, all coefficients, log likelihood, and number of iterations run until termination. Additional assessment is often done using ROC, LIFT, and Logistic Regression Prediction Operator results.
See the Official MADlib documentation for elastic net regularization for more information.
- Data Output
- None.