Aggregation Methods for Batch Aggregation

In contrast to the Aggregation operator, which forces you to configure each aggregation separately, with the Batch Aggregation operator, you can select many numeric columns for each aggregation method and computes all these aggregations at once. The result is a wide dataset that contains the grouping column and a column for each of the aggregations.

Available Aggregation Methods
Aggregation Parameter Name Prefix/Suffix Formula Performance Implications
Count group_size The number of non-null members of this group.
Minimum min The lowest value in each group.
Maximum max The highest value in each group.
Sum sum The sum of all of the values in each group.
Mean mean Sum/Count for each group. Online calculation performed using Spark SQL
Variance var The population variance:

avg(col*col)-avg(col)*avg(col)

Online calculation performed using Spark SQL (v 1.5.1)
Standard Deviation sd The square root of the above. Online calculation performed using Spark SQL (v 1.5.1)
Distinct distinct The number of distinct values in the group. Calculated using Spark SQL (v 1.5.1) Slow if there are many distinct values within each group, or if no group was selected.
Median1 median The middle element of the group. Specifically, we calculate median as the nth largest element in the group where
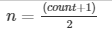median for batch aggregation

 Expensive. Unlike the other values, cannot be calculated using highly performant Spark SQL optimizer. Requires an additional shuffle step. Might reach memory limitations if there are many groups.
Related concepts
Related tasks
1 This definition varies slightly from the formal definition of median. In cases where the number of elements is odd, the answer is the same. Usually the median averages the two middle elements, but we select the one at the count/2 position. Our answer might be lower than an averaged answer, depending on the range of the data. For example, suppose that the values in one group are (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Using count/2 to select the middle position, we get the fifth element, which is 4. Other statistical packages might calculate it as AVG(4,5) = 4.5. Our method of getting median is somewhat faster for distributed data, and on large data this difference is negligible.