Correlation and Covariance

Correlation and covariance are statistical mathematical expressions that describe the degree at which two random variables or sets of random variables change their values in similar ways.

You can explore correlation and covariance and learn more about the operator algorithm by reading the help for the Correlation operator (either DB or HD).

Correlation

The correlation between two random variables is a statistical measure of the relationship between the movements of the two variables. This relationship, which is expressed by what is known as the correlation coefficient, is represented by a value between -1.00 and +1.00.
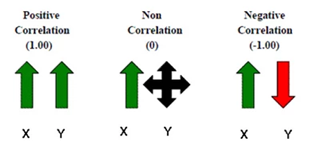
  • A correlation coefficient of +1.00 indicates that two variables move in the same direction at all times. If variable X gains in value, we would expect variable Y to gain in value as well.
  • A correlation coefficient of 0 indicates that the movements are totally random; that is, a gain by variable X provides no insight into the expected movement of variable Y.
  • A correlation coefficient of -1.00 indicates that the two variables move in opposite directions at all times. If variable X gains in value, we would expect variable Y to decrease in value.

    The following image illustrates these relationships:

Correlation illustration

Covariance

The covariance between two random variables is a statistical measure of how much the variables change together. Covariance is similar to the correlation algorithm, but without the data normalization.

  • If the variables show similar changes, the covariance is positive.
  • If the variables show opposite behavior, the covariance is negative.
  • The sign of the covariance shows the tendency in the linear relationship between the variables.
  • The magnitude of the covariance is not easy to interpret.

Variance is a special case of covariance, in which the two attributes are identical (that is, the covariance of an attribute with itself).

Note: Both the DB and HD operators can calculate the covariance.
Related concepts