Principal Component Analysis
PCA, or Principal Component Analysis, is a multivariate technique for examining relationships among several quantitative variables. It uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables (principal components).
See PCA Configuration (DB) for information about using PCA with a database data source. See PCA Configuration (HD) for information about using PCA with a Hadoop data source.
The main reason for using the PCA modeling technique is to create a mapping from the original N dimensions of a large dataset to a new set of a smaller, n dimensions (where n is usually a significantly smaller number than N).
- The principal components represent the axes (or unit vectors along the axes) of the new dimensions.
- The principal components are ordered, such that the first component contains the most variation from the original dataset.
- In other words, if the original dataset is mapped onto just the first component, the least information is lost compared to mapping it onto any other component.
Unlike attribute subset selection, which reduces the attribute set size by retaining a subset of the initial set of attributes, PCA "combines" the essence of attributes by creating an alternative, smaller set of variables. The initial dataset is therefore projected onto this smaller set.
PCA uses fewer principal components to replace original variables in analysis which often reveals relationships that were not previously suspected and thereby allowing interpretations that would not ordinarily result.
- PCA is then often the first step of the data analysis (as a method for dimensionality reduction), followed by discriminant analysis, cluster analysis, or other multivariate techniques.
- It is thus important to find those principal components that contain most of the information.
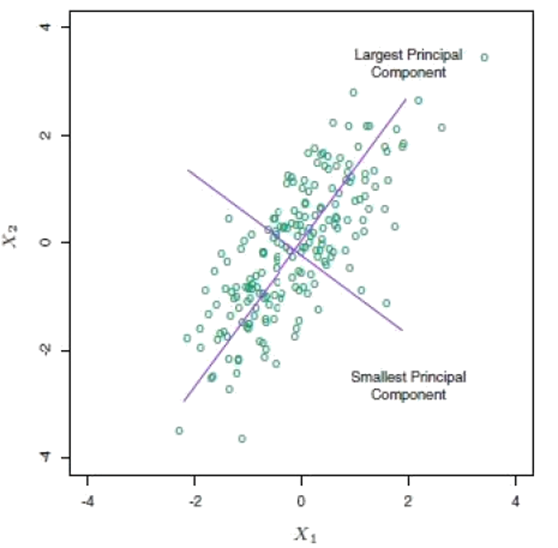
- The following figure shows the principal components of some data points in two dimensions. The largest principal component runs along an axis that shows the greatest variation of the data and would represent the first principal component. The smallest principal component shows the least data variation.
Creating PCA workflows varies depending if the analysis is being done against a database or a Hadoop data source, as follows:
- The PCA Operator for database both analyzes the data for principal components, defines the data mapping and also transforms the data (by applying the mapping) to be passed into any other modeling Operator directly.
- The PCA Operator for Hadoop analyzes the data for determining the principle components and defines the data mapping but needs the PCA Apply Operator to transform the data (by applying the mapping) before passing the reduced variable set into any other modeling Operator.
- The PCA Apply Operator for Hadoop applies the data mapping. It can be applied to either new, updated datasets (with the same column names) or to the source training dataset (whereas the PCA Operator for database can only be applied to the training dataset).