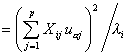Principal Components and Classification Analysis - Computational Details
This section provides the computational details and the formulas that were used in the implementation of the Advanced Principal Components Analysis in this module.
- Data
- Consider a data set of p active and k supplementary variables and n active and m supplementary cases. The data pertaining to the active variables and active cases can be arranged in the matrix, X, of n rows and p columns:
where Xij represents the value of the j th variable for the i th case, standardized or centered about their respective means. Similarly, the data pertaining to the supplementary variables can be arranged in the matrix Y of n rows and k columns:
where Yit is the value of the t th supplementary variable for the i th case, standardized or centered about their respective means. The data pertaining to m supplementary cases can be arranged in the matrix Z of m rows and p columns:
where Zls is the value of the s th variable for the l th case, standardized or centered about their respective means.
- Symmetric Matrix to be diagonalized
- The orthogonal set of vectors are obtained by diagonalizing the matrix.
X'X is the correlation matrix, if the values are standardized.
X'X is the covariance matrix, if the values are centered about their means, where X' is the transposed data matrix
- Eigenvalues and Eigenvectors
- Denote the set of q positive eigenvalues of the matrix
X'X (correlation or covariance) as:
Denote the set of q eigenvectors corresponding to q eigenvalues as:
- Quality of representation
- Quality of representation of first s principal components:
- Factor coordinates of active variables
- a th factor coordinate of the j th active variable:
- Factor coordinates of supplementary variables
- a th factor coordinate of the t th supplementary variable:
where Yti is the (t, i) th element of the transpose of the matrix Y for k supplementary variables and p in the summation sign is the number of active variables.
- Factor & variable correlation
- Correlation between a th factor and the j th variable:
Communalities (Cosine2). a th communality of the j th variable:
Contributions of variables.
Relative contribution of the j th variable to the variance of the a-factor axis:
- Factor coordinates of active cases
- a th factor coordinate of the i th active case:
- Factor coordinates of supplementary cases
- a th factor coordinate of the s th supplementary case:
where Zsj is the (s,j) th element of the matrix Z for m supplementary cases, and p in the summation sign is the number of active variables.
- Factor score coefficients
- l th factor score coefficient corresponding to a th factor:
- Factor scores
- Factor score of the i th case for the a th factor:
Cosine2 of cases. Cosine square of the i th case for the a th factor:
where pi2 is the normalizing constant, obtained by summing all the factor coordinates of the i th case. The element Uij comes from the X or Z data matrix, depending upon whether the case is active or supplementary.
- Contributions of cases (active)
- Contribution of the i th active case for the a th factor:

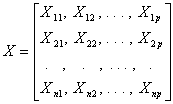
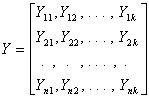

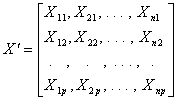
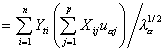 ,
,
 ,
,