Non-Normal Distributions - Beta Distribution
The Beta distribution has the probability density function:
f(x) = Γ(ν+ω)/(Γ(ν)Γ(ω)) * xν-1 * (1-x)ω-1
0 < x < 1, ν > 0, ω > 0
where
| Γ | (Gamma) is the Gamma function |
| ν, ω | are parameters |
(Note that the shape of the Beta distribution depends on the values of the parameters as shown in the animation below; for more information, see Hahn and Shapiro, 1994.)
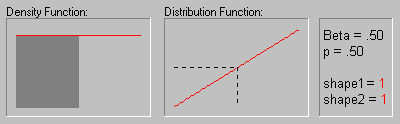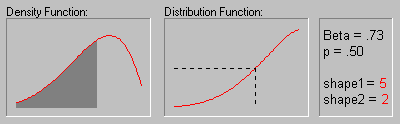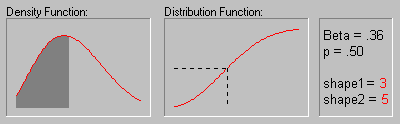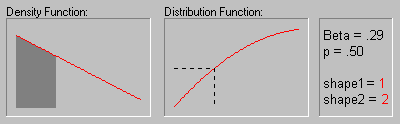
Threshold (location) and sigma
The standardized Beta distribution has a valid range from 0 to 1. However, you may specify a lower threshold (location) parameter and a scale parameter (Sigma); the program will then fit the Beta distribution to the standardized variate computed as:
(x-location)/Sigma
Copyright © 2021. Cloud Software Group, Inc. All Rights Reserved.
