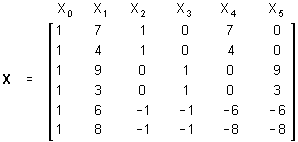GLM Introductory Overview - Homogeneity of Slopes
The appropriate design for modeling the influences of continuous and categorical predictor variables depends on whether the continuous and categorical predictors interact in influencing the outcome. The traditional analysis of covariance (ANCOVA) design for continuous and categorical predictor variables is appropriate when the continuous and categorical predictors do not interact in influencing responses on the outcome, and the separate slope design is appropriate when the continuous and categorical predictors do interact in influencing responses. The homogeneity of slopes designs can be used to test whether the continuous and categorical predictors interact in influencing responses, and thus, whether the traditional ANCOVA design or the separate slope design is appropriate for modeling the effects of the predictors. For the same example data used to illustrate the traditional ANCOVA and separate slope designs, the overparameterized X matrix for the design that includes the main effect of P, the main effect of the three-level categorical predictor A, and the 2-way interaction of P by A would be
If the b5, b6, or b7 coefficient in the regression equation
Y = b0 + b1X1 + b2X2 + b3X3 + b4X4 + b5X5 + b6X6 + b7X7
is non-zero, the separate slope model should be used. If instead all 3 of these regression coefficients are zero the traditional ANCOVA design should be used.
The sigma-restricted X matrix for the homogeneity of slopes design would be
Using this X matrix, if the b4, or b5 coefficient in the regression equation
Y = b0 + b1X1 + b2X2 + b3X3 + b4X4 + b5X5
is non-zero, the separate slope model should be used. If instead both of these regression coefficients are zero the traditional ANCOVA design should be used.
Between-subject designs
Within-subject (repeated measures) designs
Multivariate designs