Noncentrality-Based Indices of Fit - Noncentrality-Based Parameter Estimates and Confidence Intervals

Let S be the sample covariance matrix based on N observations, and for notational convenience, define n = N - 1. S(q) is the attempt to reproduce S with a particular model and a particular parameter vector q. S(qML) is the corresponding matrix constructed from the vector of maximum likelihood estimates qML obtained by minimizing the discrepancy function of Equation 56. Equations 56 and 58 give two alternative discrepancy functions which lead to Chi-square statistics for testing structural models. Suppose one has obtained maximum likelihood estimates. Then under conditions (i.e., the "population drift" conditions in Steiger, Shapiro, and Browne, 1985) designed to simulate the situation where the model fits well but not perfectly, n FML(S, S(q)) has an asymptotic noncentral Chi-square distribution with p(p + 1)/2 - t degrees of freedom, where t is the number of free parameters in the model, and p is the order of S. The noncentrality parameter is n F* = n FML(S, S(q)). F* is the value of the statistic in Equation 56 obtained if S is replaced by the population covariance matrix S, and maximum likelihood estimation is performed on S instead of S. Hence, for the quadratic form statistic, the noncentrality parameter is in effect the "population badness-of-fit statistic."

Interestingly, if one divides by the noncentrality parameter by n, one obtains a measure of population badness-of-fit which depends only on the model, S, and the method of estimation.

If one has a single observation from a noncentral Chi-square distribution, it is very easy to obtain an unbiased estimate of the noncentrality parameter. By well known theory, if noncentral Chi-square variate X has noncentrality parameter l and degrees of freedom n, the expected value of X is given by

E (X) = n + l(88)

whence it immediately follows that an unbiased estimate of l is simply X - n. Consequently a large sample "biased corrected" estimate of F* is
 (X - n)/n. Since F can never be negative, the simple unbiased estimator is generally modified in practice by converting negative values to zero. The estimate

    (89)

is the result.

It is also possible, by a variety of methods, to obtain, from a single observation from a non-central Chi-square distribution with n degrees of freedom, a maximum likelihood estimate of the noncentrality parameter l, and confidence intervals for l as well. (See, e.g., Saxena and Alam, 1982; Spruill, 1986.)

Before continuing, recall some very basic statistical principles.

  1. Under very general conditions, if is a maximum likelihood estimator for a parameter q, then for any monotonic strictly increasing function f ( θ), 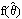is a maximum likelihood estimator of .
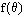  2. Moreover, if clow and chigh are valid limits of a 100(1-a)% confidence interval for q, f(clow) and f(chigh) are valid limits of a 100(1-a)% confidence interval for .

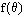These principles immediately imply that, since one can obtain a maximum likelihood estimate and confidence interval for n F*, one can obtain a confidence interval and maximum likelihood estimate for F* by dividing by n.

SEPATH obtains a point estimate and confidence interval for n F* by iterative methods. The 100(1-a)% confidence limits for the noncentrality parameter l of a χ 2ν ,λ distribution are obtained by finding (via quasi-Newton iteration) the values of l which place the observed value of the Chi-square statistic at the 100(a/2) and 100(1-a/2) percentile points of a χ 2ν ,λ distribution. The "point estimate" of the "population noncentrality index" printed by SEPATH is the simple bias-corrected estimate F+ (see Equation 89) recommended by McDonald (1988).

When the IRGLS or GLS estimation methods are employed, the population noncentrality index is a quadratic form, and as such is a weighted sum of squares of the residuals. Suppose you were to place the non-redundant elements of S in a vector s = vecs (S). Recalling the result of Equation 67, the discrepancy function is of the form e'We, i.e., a weighted sum of squared discrepancies.